|
* u+ S* L& q; G: f) l -点击上方“覆盖区找矿”关注,精彩更多… 1 p- z& o0 x, p9 [6 W) Y' s& E

0 {' }" l! t6 M; U( P: F
“强烈的爱国情怀,是保持创新的活水渊源,浓厚的科学兴趣,是不懈探索的持久动力”。——殷长春
_) }2 w+ ^0 d; ? 基于区域分解法的海洋可控源电磁三维正演模拟研究 殷长春1,张文强1,2*,苏扬1,张博1,刘云鹤1,邱长凯3,惠哲剑11吉林大学地球探测科学与技术学院2 中国电子科技集团公司第五十八研究所
! y% ? p( \# j" K! ?6 [ 3 中国地质调查局发展研究中心 ! g8 q# I5 P3 j$ {6 B
第一作者简介,殷长春(简介附后)
4 ~% z+ _6 |) S6 }) h4 D% T4 e6 I 通讯作者,张文强,硕士,主要从事海洋电磁正反演研究 导读:海洋蕴藏着丰富的油气资源。海洋可控源电磁法是一种有效的海洋油气勘探方法,可为钻前储层预测和评价提供重要依据。然而,在构造复杂区域勘探时,模拟海底地质结构电磁响应的正反演计算需要求解百万以上大型方程组,耗费大量计算资源。为此,正反演方法创新成为众多学者研究热点。殷长春教授等将区域分解算法引入到海洋电磁三维正演模拟计算中,创新了正演模拟技术方法,不仅有较高的计算精度,还节省了计算内存。对地球物理其它方法正演模拟研究也有参考作用。该方法首先利用非结构四面体网格对海洋地电模型进行离散,而后使用METIS剖分软件将网格分区得到一定数量的子区域并建立相应的边界条件,然后基于矢量有限元法建立各子区域的正演问题,进而将各子区域耦合到到降阶的子系统,求解该子系统后即可求到任意子区域内的电磁响应。并利用海底均匀半空间模型验证了算法的精度和有效性,并在此基础上对典型的复杂海底介质模型的电磁响应进行正演模拟。数值结果表明,该算法是进行海洋可控源电磁正演模拟研究的有效方法,可以解决大规模海洋电磁正演问题。研究成果具有重要意义!! S& |: V! P5 b9 f; g! N% j
内容提纲 0 引言1 正演理论2 精度验证3 数值算例3.1 马鞍形高阻体模型3.2 盐丘模型4 结论4 E9 e R5 d& O
0引言 海洋蕴藏着丰富的油气资源,为缓解日益增长的能源资源需求与供给不平衡问题,加大对海洋油气资源的勘探势在必行。海洋可控源电磁法(Marine Controlled-Source Electromagnetic Method,简称MCSEM)作为钻前储层预测和评价的有效方法,已广泛应用于海洋油气勘探中。该方法是近年来众多学者关注的热点领域,在正反演理论上也得到长足的发展。然而,随着研究问题的复化,特别是勘探工作由构造相对简单区域向复杂区域延伸,为有效模拟复杂海底地质结构条件下电磁响应特征,必须采用精细网格对海底构造展行模拟,由此导致需要求解几百万甚至千万未知数的大型方程组。求解如此大规模问题需要耗费大量的计算资源。学者们研究了各种新方法以解决这一问题,区域分解(Domain Decomposition Method,DDM)就是其中的一种方法。区域分解法是将计算区域划分为若干子区域,分别求解再展行综合的一种数值计算方法。其核心思想是将原先的大型问题,分解为若干个小型问题,缩小计算规模,减少内存需求。区域分解法起源于论证非规则椭圆型方程的存在与唯一性的Schwarz交替方法,而Lions(1988,1989)提出的Schwarz交替方法的投影解释奠定了区域分解法的基础。此后,众多学者对区域分解法展行深入的研究,并将其应用到计算力学、计算电磁学、医学成像等领域。在电磁领域,Després(1991)首先将基于节点有限元的非重叠型Schwarz交替算法用于求解电磁问题,并通过在子区域交界面上施加Robin类型传输条件来保证子区域之间电磁场的连续性。Stupfel(1996)和Gander等(2002)在Despres(1991)的基础上通过对边界条件进行优化,改善了迭代解释的收敛性。Farhat和Roux(1991)提出了基于Lagrange乘子的有限元撕裂-对接法(Finite-Element Tearing and Interconnecting,FETI)。该方法的特点是利用Lagrange乘子在子区域交界面上施加连续性边界条件。为解决Lagrange乘子在子区域交界面上的冗余题,Farhat等(2001)提出了FETI-DP (Dual-PrimalFinite-ElementTearingandInterconnecting)方法,并将其应用于求解亥姆霍兹方程取得了良好的效果。由于FETI-DP方法是基于节点有限元法提出的,为更好地求解电磁问题,Li和Jin(2006)提出了基于矢量有限元的FETI-DPEM方法,成功实现了大天线结构的电磁求解问题,此后该方法在计算电磁领域被广泛用到于大规模正演题的求解。然而,目前区域分解法在地球物理领域中的应用相对较少。李丹等(2017)基于Schwarz重叠型区域分解法实现二维大地电磁正演模,Xiong(1999)和Silva等(2010)分别基于有限差分法的重叠型Schwarz法和Schur补区域分解法实现了三维可控源电磁问题的正演模拟,Ren等(2014)利用区域分解法实现了三维大地电磁问题正演模,而周远国(2017)将谱元法与区域分解法相结合实现了三维航空电磁正演模模拟。区域分解法作为一种求解大规模数值模拟的有效方法,将在地球物理问题愈发复杂化及计算规模激增的条件下发挥重要作用。本文基于矢量有限元法的FETI-DP区域分解法开展海洋可控源电磁三维复杂模型正演模拟研究。我们首先介绍基于FETI-DP区域分解法的MCSEM正演理论,并利用一维半空间模型对其进行精度验证,最后我们通过对典型海底模型的电磁响应进行模拟,以验证本文算法在海洋可控源电磁三维复杂模型正演模拟中的有效性。! W: b# M- v: h( t/ n4 \
1正演理论 假设时谐因子为,在忽略位移电流条件下由麦克斯韦方程可得: 式中,E为电场强度,Js表示发射源项,ω=2πf,f为频率,ρ为电导率,μ为磁导率(假设为真空磁导率μ0),使用COMSOL将计算区域Ω离散为一系列非重叠的四面体网格,并用一阶Nédélec矢量基函数对单元内的磁场展优插值,则每个四上体单撕内磁场控近似为: 式中,E为电场强度,Js表示发射源项,ω=2πf,f为频率,ρ为电导率,μ为磁导率(假设为真空磁导率μ0),使用COMSOL将计算区域Ω离散为一系列非重叠的四面体网格,并用一阶Nédélec矢量基函数对单元内的磁场展优插值,则每个四上体单撕内磁场控近似为: 其中,Nj是第j条棱边的矢量基函数,Ej是第j条棱边的切向磁场。为保证电场求解的唯一性,我们需要给出外边界∂Ω上的边界条件。假设求解区域外边界∂Ω离场源足够远,则可以在其上施加Dirichlet边界条件,即: 其中,Nj是第j条棱边的矢量基函数,Ej是第j条棱边的切向磁场。为保证电场求解的唯一性,我们需要给出外边界∂Ω上的边界条件。假设求解区域外边界∂Ω离场源足够远,则可以在其上施加Dirichlet边界条件,即: 式中,n表示边界上的单位法向量。下面我们讨论子域分解问题。我们首先利用剖分软METIS将整个计算区域Ω划分为N个互不重叠的子域,进而根据伽辽金法建立每个子域的正演问题。以第s个子区域Ωs为例,在Ωs内部存在如下边值部题: 式中,n表示边界上的单位法向量。下面我们讨论子域分解问题。我们首先利用剖分软METIS将整个计算区域Ω划分为N个互不重叠的子域,进而根据伽辽金法建立每个子域的正演问题。以第s个子区域Ωs为例,在Ωs内部存在如下边值部题: 当一个解法域分被分分为若干个子区域时,需要保证子区域域间电磁场的连续性。在子区域s与子域q的交界面Γsq上需要满够下边两个界界件来: 当一个解法域分被分分为若干个子区域时,需要保证子区域域间电磁场的连续性。在子区域s与子域q的交界面Γsq上需要满够下边两个界界件来: 其中ns和nq分别为子域s和子域q的外法线方向上的单位向量。我们利用矢量有限元将子区域s内的矢量场展开,并运用Galerkin方法即可获得求解子区域s的线性方程组为: 其中ns和nq分别为子域s和子域q的外法线方向上的单位向量。我们利用矢量有限元将子区域s内的矢量场展开,并运用Galerkin方法即可获得求解子区域s的线性方程组为: 式中,ES为区域s内待求的未知电场,子区域有限元矩阵Ks和源项fs的具体形式为: 式中,ES为区域s内待求的未知电场,子区域有限元矩阵Ks和源项fs的具体形式为: 每个子区域中的棱边按其所在位置可第分为两种类传:位于子域内部和子域交界面上的棱边(用r表示)以及位于拐角(corner)上的棱边(被三个或三个以上的子域共享,用c表边)按照上述了义对公式8)进优分分,并采一拉格朗日乘子λ表示公式(8)中与Λ相关的面积分项,可得: 每个子区域中的棱边按其所在位置可第分为两种类传:位于子域内部和子域交界面上的棱边(用r表示)以及位于拐角(corner)上的棱边(被三个或三个以上的子域共享,用c表边)按照上述了义对公式8)进优分分,并采一拉格朗日乘子λ表示公式(8)中与Λ相关的面积分项,可得: 我们进一步定义带符号的逻辑布尔矩阵Brs和和Bcs,分别表示子区域域内的自由度λrs、Ecs和全局自由度λ、Ec间的映射关系,即满足λrs=Brstλ及Ecs=BcsEc,则电场和磁场的切向连续条件可表示为: 我们进一步定义带符号的逻辑布尔矩阵Brs和和Bcs,分别表示子区域域内的自由度λrs、Ecs和全局自由度λ、Ec间的映射关系,即满足λrs=Brstλ及Ecs=BcsEc,则电场和磁场的切向连续条件可表示为: 由此,我们可以将各子区域耦合起来,并选择消去去Ec以得到一个仅与交界面上的未知量入有关的子系统: 由此,我们可以将各子区域耦合起来,并选择消去去Ec以得到一个仅与交界面上的未知量入有关的子系统: 公式(13)实质上是通过区域分间的边界条件将所有子区域耦合在一起以实现区域分边界上电磁场求解。不难看出该区域是一个密实的系统,使用直接求解器进行求解会大大降低区域分解法的有效性。因此,我们采用Krylov子空间迭代方法中的广义最小残差法对公式(13)进行求解。最后,通过将子区域边界上电磁场作为边界条件即可对各子区域内的电磁场进行求解,从而实现整个计算区域电磁场的求解。本文中,为了有效利用广义最小残差法求解电磁问题,我们选用如下形式的Dirichlet预条件子,以改善GMRES迭代求解器的收敛性,即:
P5 y& G4 b: a3 G _ 公式(13)实质上是通过区域分间的边界条件将所有子区域耦合在一起以实现区域分边界上电磁场求解。不难看出该区域是一个密实的系统,使用直接求解器进行求解会大大降低区域分解法的有效性。因此,我们采用Krylov子空间迭代方法中的广义最小残差法对公式(13)进行求解。最后,通过将子区域边界上电磁场作为边界条件即可对各子区域内的电磁场进行求解,从而实现整个计算区域电磁场的求解。本文中,为了有效利用广义最小残差法求解电磁问题,我们选用如下形式的Dirichlet预条件子,以改善GMRES迭代求解器的收敛性,即:
P5 y& G4 b: a3 G _ 
其中,ε为后验误差,A、f分别表示公式(13)中的左端项矩阵和右端项。值得注意的是,区域分解法的实现过程非常灵活,在迭代求解时各系数矩阵可预先采用直接求解器PARDISO或MUMPS进行分解以加速迭代过程。) r1 b, {: O5 @ B/ ]
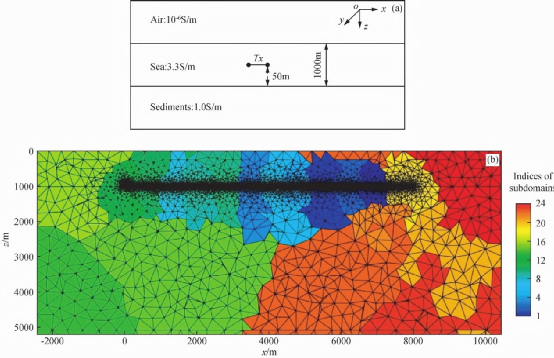
2精度验证 为验证本文算法的精度,我们设计了如图1所示的水平海底半空间模型。假设海水深度1000m,电导率3.33 S/m。海底介质电阻率1 S/m,空气层的电导率设为10-6S/m。发射源长度为100m,位于海底上方50m,发射频率为0.25Hz,共计80个测点位于海底,与发射源同线分布,相距100m。对计算域进行网格剖分得到297232个四面体单元,采用METIS对该网格进行分区,共分为24个子区域,交界面上未知量λ的数目为20197。图1中网格单元的不同颜色代表其所属子域编号。6 s* a4 Y4 Z3 U0 K$ v
' O- |! ]1 L1 h
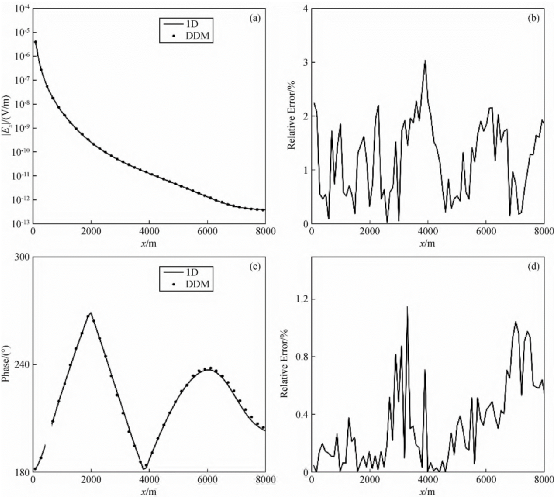
图1 水平海底半空间拟型及科区分剖分网格截面图 需要指出的是,采用METIS进行子区域划分的过程,实际上是将原始子区域划分转变为图形划分问题,因而划分结果不受网格单元物性的影响,各子域实际大小与子区域内网格单元的大小相。本文所有的数值计算都在Inter(R)Xeon(R)E5-2667V4@3.2GHzCPU和128GB内存的工作站上完成。图2给出本文结果(DDM)和一维半解析解的对比。由图可以看出,两种方法计算结果吻合的很好,振幅最大误差3.1%,相位最大误差1.2%,说明本文算法具有较高的计算精度。$ n- F$ ^9 S6 ?
, Y" }! e5 E: ^! U. D/ Q; a1 H
图2 本文算法与一维半解析解的结果对比
- t( ^7 g R4 Q/ u (a)电场MVO曲线;(b)振幅相对误差曲线;(c)电场PVO曲线;(d)相位相对误差曲线 0 P) ?( M* n5 P3 p! B3 o0 E- j) ?
3数值算例
$ q* i6 P9 b! m, \8 s3 D 3.1马鞍形高阻体模型 下面我们模拟海底存在马鞍形高阻体和带地形的岩丘模型的海洋电磁响应,以检验本文算法进行MCSEM大规模问题演模拟研的有效性。我们设计如图3所示的马鞍形背斜圈闭,x方向大小为3680m,y方向大小为2000m,圈闭最厚处150m,电导率为0.01 S/m。异常体上顶面距海底800m,下底距海底2020m。海水深度1000m。电导率3.33 S/m,围岩和空气层的电导率分别为1 S/m和1.0X10-6 S/m。发射源长100m,位于海底上方50m,发射频率为0.25Hz。测点与发射源同线分布,相距100m,共80个。
% m, h; n" a4 T 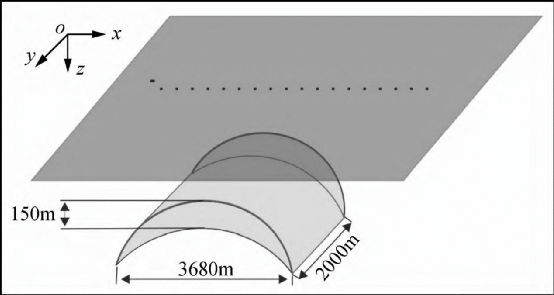
7 l a; Y. `6 A# a- G
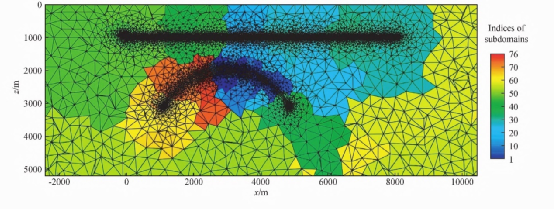
图3水平海底马鞍形高阻异常体模型 对图3所示的模型进行四面体网格剖分,得到776557个四面体单元。然后,我们使用METIS将四面体网格划分为76个子域,交界面上未知量λ的数目为62969。分区结果如图4所示。+ g* X6 @' k7 e" m/ A1 V
& y) ~: I; R1 \: c/ l2 ^
图4 水平海底马鞍形高阻体模型分区截面图 图5展示了本文分区算法与采用MUMPS直接求解器的结果对比。由图可以看出,本文算法与Zhang等(2018)的计算结果振幅最大相对误差1.5%,相位最大相对误差1.2%,说明本算法的具有较高的计法精度。
$ m7 j2 k- a3 V/ T% C0 Q* l6 ` 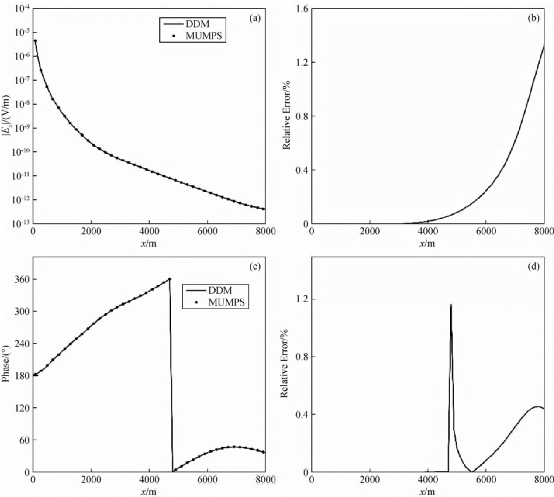
7 y/ C3 A; N, g( c7 {
图5本文算法与Zhang等(2018)结果对比
# R2 G. ~) h5 Q/ t% U (a)电场MVO曲线;(b)振幅相对误差曲线;(c)电场PVO曲线;(d)相位相对误差曲线 为探究本文算法对计算资源的需求,我们统计了针对图3所示的模型,分别利用本文算法和采用求解器MUMPS算法在计算内存和计算时间上的误差对比结果。本文算法中GMRES求解器的重启次数设置为50,经150次迭代收敛。由表1可以看出,在相同网格情况下,区域分解法通过牺牲计算时间的方式减少了求解过程中的内存需求,本质上属于以径间换空间的方法。考虑到在小型计算设备上,内存需求有时对三维电磁正反演来说起更关键的作用,因此本文算法为实现有限计算资源条件下大规模海洋电磁正演打下基础。1 j$ K) L& d7 N4 \
表1 区域分解法与MUMPS计算资源需求对比 4 {! A$ X/ ~6 e/ l/ x

. Y! J9 v9 p% e 3.2盐丘模型 为模拟实际复杂海底地质结构条件下海洋可控源电磁响应,我们参照Aminzadeh等(1994)设计了图6所示的起伏海底盐丘模型。盐丘的电导率为0.01 S/m,围岩的电导率为1 S/m,起伏海底最深1000m,最浅500m。发射源长100m,位于海底上方50m,发射频率为0.25Hz。接收机布设于起伏海底,相距100m,共80个。图6也给出了该模型的网格剖分结果。我们将模型剖分成1285511个四面体单元。利用METIS将模型剖分为110个子区域,交界面上未知量λ的数量为108462。
# p0 U8 ]' R. w 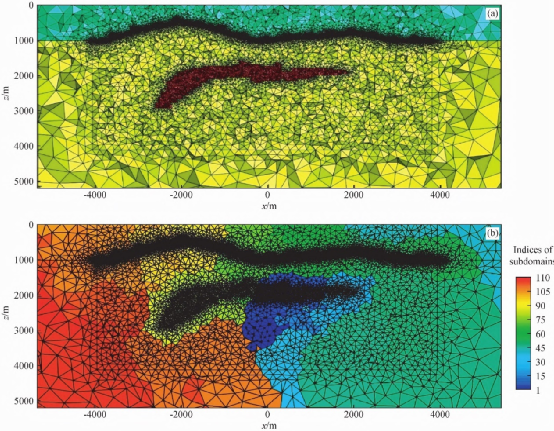
- G7 {$ p5 a r7 | { 图6起伏海底盐丘模型网格剖分及分区结果 针对图6的模型,我们分别模拟了半拖曳、全拖曳和CT扫面观测时的海洋可控源电磁响应。图7出了本半拖曳观测方式同线电场响应,共设计15组发射源,距离海底50m,发射源位置从-3520m到3520m,间距500m,发射频率为0.25Hz。从图可以看出,海底存在异常体时在电磁响应上有明显的反应,这说明海洋可控源电磁法对高阻异常体有很好的探测能力。
[3 C% S% ?" O$ V: w6 n" } ^ 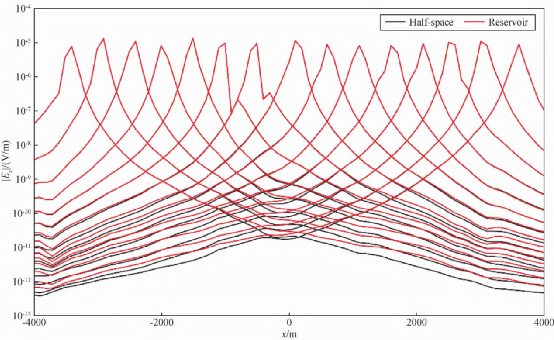
N2 n* a/ ` i4 j 图7 图6给出的盐丘模型同线电场及与半空间(无盐丘)响应对比 图8给出了针对图7所示模型采用全拖曳电磁观测方式计算的同线电场。发射源距离海底50m,发射频率为0.25Hz,接收机位于海底上方30m,发收据为6000m。由图8可以看出,高阻盐丘同样在电场响应中有明显的反应,且相比于半拖曳式电磁探测,全拖曳式电磁探测高阻异常体影响范围更宽,幅值差异更大,为反演解释工作提供了有力支撑。然而,必须指出:考虑到电磁探测深度与发收距和频率密切相关,在全拖曳式海洋电磁探测中,为获得较好的垂向探测效果,建议使用多个发收距重复测量或者进行多频探测。
$ T8 E, w- [2 @. v5 h 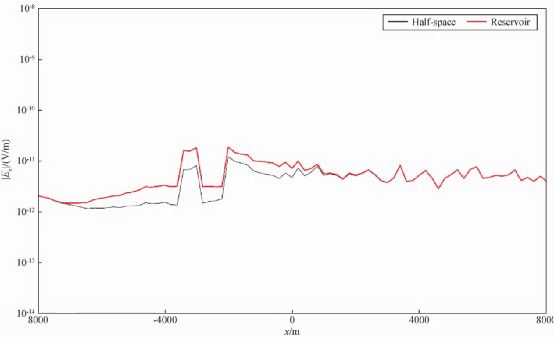
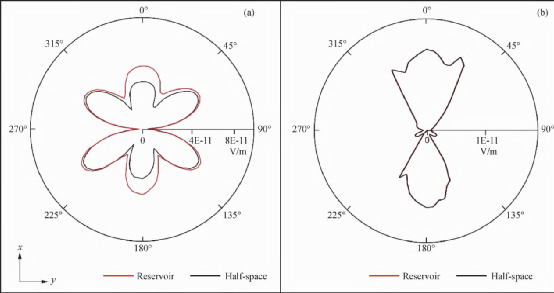
- R1 [$ ~+ f; h+ f, L+ K- S; ? V 图8全拖曳观测方式同线电场分布 最后,我们模拟了全拖曳式海洋电磁CT扫面观测时针对图7所示模型的海洋电磁响应。发射源距离海底50m,发射率为为0.25Hz。以发射源中心为坐标原点,测点位于海底上方30m处,距离发射源保持3000m。图9给出了径向电场的极性分布,图中从原点到各测点连线的长度表示径向电场值的大小,连线的方向代表观测的径向电场方向。我们假设测点间隔为5°,共计70个测点。由图9可以看出,径向电场的分布明显反映出地下盐丘在x、y平面的展布特征。盐丘在x方向展布较大,y方向展布较小,特别在径向电场差值的极性图上得到很好的反应。8 n; p% s0 a ]4 y- Q5 T5 t7 y# q' ^1 @
& m, f& [2 r) Y, J. F0 t- H
图9海洋电磁CT扫面观测时径向电场分布 7 |! G, j2 M# ^
(a)径向电场;(b)存在和不存在高阻异常体的径向电场差 根据径向电场在各个角度与半空间结果差异程度,我们即可定性判断异常体在该方向的展布,为后续反演工作选择合适的模型提供前提。$ ~6 b3 Q+ H: `' x( z( B+ |1 k
4结论 本文成功将基于矢量有限元的非重叠型区域分解法应用到海洋可控源电磁正演模拟中,通过和层状介质半解析解对比验证了本文算法的精度和有效性。进而,通过和三维有限元直接求解结果对比,可以看出本文算法不仅具有较高的计算精度,同时也可节省计算内存,未来结合各种并行技术可以期望本方法为求解大规模海洋电磁正演问题提供一种有效的途径。数值模拟结果表明,本文算法适用于多种海洋电磁观测方式,因此为全拖曳式海洋电磁系统正演模拟打下基础。考虑到采用多种方式联合观测可以有效地获取地下高阻异常体的详细信息,建议条件容许时采用多种观测方式对海底目标体进行多种方式探测,为后续海洋电磁数据反演解释提供有力的支撑。致谢 感谢审稿专家对本文提出的宝贵修改意见!来源:殷长春,张文强,苏扬,等.2022.基于区域分解法的海洋可控源电磁三维正演模拟研究.地球物理学进展,37(1):0469-0477.导读评论和排版整理等:《覆盖区找矿》公众号.推荐读者下载、阅读和引用原文!
+ b7 o2 h0 x7 u* j0 v4 `& W ---------殷长春介绍---------- ) F, R1 S: ^7 [7 j, u. m8 M

殷长春,教授,博导,吉林大学移动平台地球物理研发中心主任。主要从事电磁法勘探理论模拟和应用技术研究。先后承担国家自然科学基金重点和面上项目、国家863重大项目、国家重大仪器专项课题十余项,担任国家重点研发计划项目的首席科学家。在国际一流地球物理杂志发表论文120余篇,获得吉林省优秀外国专家奖、中国科学院杰出科技成就奖、中国地球物理科技创新和技术进步奖(各一项)、中国地球物理学会陈宗器优秀论文奖、中国地球物理学会工程地球物理优秀论文奖(两项),美国SEG Bright Spot Paper奖等。2019年被评为吉林省有突出贡献专业人才。------------往期精彩回顾-------------4 Q# ~& s1 d% P+ |
林君,薛国强,李貅:地-空电磁探测技术方法,发展现状与创新思考
& ^, G3 E" G1 z 曾昭发:深部金属矿综合地球物理响应与综合预测方法 , ]( _' B" y% {1 P% Z9 i. Q
地质找矿与工程勘察都有效:井间电磁法新进展
5 \! N2 W) O2 F 地球物理三维电磁反演方法研究动态
) b/ n3 l a; i7 j: ^9 a 大洋富钴结壳矿研究进展与展望 1 L/ E( K7 d% D
------关注“覆盖区找矿”,拥有更多新方法------
) ^/ }9 H( v; B  fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)
Y4 m- E* j4 I: W6 H: o+ A8 z/ L 宣讲成果,助力转化,激励创新!
" y2 I2 [1 J: W2 L+ n( \; K9 z4 r% d: n0 m1 \' P
. `. I1 w: X' b4 d
+ Y) u* E8 e) n; L: ?$ ~1 H$ L- C5 j i! F
) d; S( L6 A* M
| 

