# {1 T9 e; |8 h8 y9 A/ K8 R
1гҖҒд»Җд№ҲжҳҜж®ӢдҪҷеә”еҠӣ?
1 ^. l2 ^0 {+ r# C6 o, V# F3 d# e
ж®ӢдҪҷеә”еҠӣ (Residual Stress) жҳҜе·Ҙ件еңЁеҲ¶йҖ иҝҮзЁӢдёӯпјҢе°ҶеҸ—еҲ°жқҘиҮӘеҗ„з§Қе·Ҙиүәзӯүеӣ зҙ зҡ„дҪңз”ЁдёҺеҪұе“Қ;еҪ“иҝҷдәӣеӣ зҙ ж¶ҲеӨұд№ӢеҗҺпјҢиӢҘжһ„件жүҖеҸ—еҲ°зҡ„дёҠиҝ°дҪңз”ЁдёҺеҪұе“ҚдёҚиғҪйҡҸд№ӢиҖҢе®Ңе…Ёж¶ҲеӨұпјҢд»ҚжңүйғЁеҲҶдҪңз”ЁдёҺеҪұе“Қж®Ӣз•ҷеңЁжһ„件еҶ…пјҢеҲҷиҝҷз§Қж®Ӣз•ҷзҡ„дҪңз”ЁдёҺеҪұе“Қе°ұжҳҜж®ӢдҪҷеә”еҠӣгҖӮ
' O4 D& U m4 p жңүзӮ№жҷ•?йӮЈжҚўдёӘйҖҡдҝ—зҡ„ж–№ејҸи·ҹеӨ§е®¶и®ІгҖӮжҜ”еҰӮиҜҙдёҖдёӘдәәд№ӢеүҚеҫҲзҳҰпјҢд№°дәҶдёҖжқЎLеҸ·зҡ„зүӣд»”иЈӨпјҢ然иҖҢиҝҮдәҶдёӘе№ҙеҗғжҲҗдәҶеӨ§иғ–еӯҗпјҢиҝҷж—¶еҖҷеҶҚз©ҝиҝҷжқЎзүӣд»”иЈӨпјҢз”ұдәҺдәәй•ҝиғ–дәҶиҖҢиЈӨеӯҗжІЎеҸҳпјҢеӣ жӯӨд»–е°ұдјҡи§үеҫ—иЈӨеӯҗеӨӘзҙ§дәҶпјҢиҝҷж—¶еҖҷиә«дҪ“дёҺиЈӨеӯҗд№Ӣй—ҙе°ұжңүдәҶеҫҲејәзҡ„дҪңз”ЁеҠӣпјҢеҰӮжһңз”ЁеҠӣиҝҮзҢӣеҫҲе®№жҳ“жҠҠиЈӨеӯҗж’•з ҙпјҢиҝҷз§Қз ҙеқҸеҠӣе°ұжҳҜж®ӢдҪҷеә”еҠӣзҡ„дҪңз”Ёж•ҲжһңгҖӮ
* w! u/ B! [3 [8 [$ s4 [$ C4 @3 S2 O# s
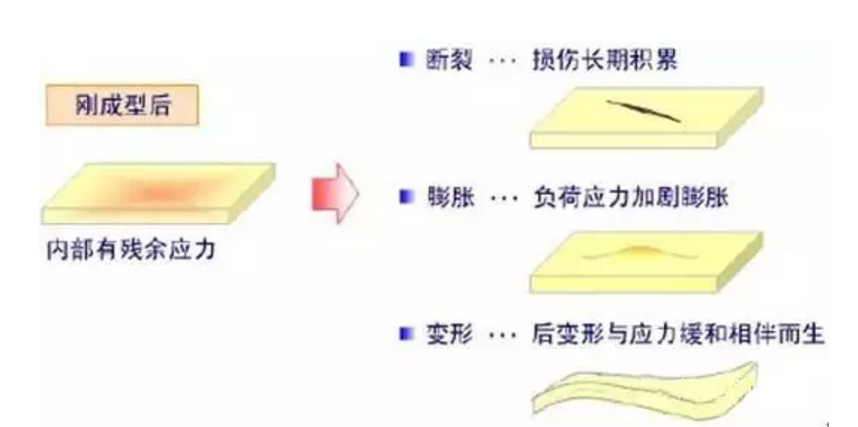
д»ҺиғҪйҮҸдҪңеҠҹзҡ„и§’еәҰжқҘзҗҶи§ЈпјҢеӨ–еҠӣдҪҝзү©дҪ“еҸ‘з”ҹеЎ‘жҖ§еҸҳеҪўж—¶дјҡеҜјиҮҙзү©дҪ“еҶ…йғЁеҸ‘з”ҹеҸҳеҪўпјҢеӣ иҖҢз§ҜзҙҜдёҖйғЁеҲҶиғҪйҮҸ;еҪ“еӨ–еҠӣж¶ҲйҷӨеҗҺпјҢеҶ…йғЁеә”еҠӣеҲҶеёғдёҚеқҮеҢҖзҡ„иғҪйҮҸиҰҒиҝӣиЎҢйҮҠж”ҫпјҢеҰӮжһңзү©дҪ“зҡ„и„ҶжҖ§дҪҺпјҢеҲҷзү©дҪ“дјҡзј“ж…ўеҸҳеҪўпјҢи„ҶжҖ§й«ҳеҲҷеҪўжҲҗиЈӮзә№гҖӮ
) I6 o' t5 l+ H* `3 ]$ S$ _
 / a2 E U3 I' z/ |4 s
/ a2 E U3 I' z/ |4 s
. s4 m A/ m/ L c/ _' E( N жү“ејҖеҮӨеҮ°ж–°й—»пјҢжҹҘзңӢжӣҙеӨҡй«ҳжё…еӣҫзүҮ
6 p. t' H8 _: v( [ # M& w6 h/ p. r8 |
еӣҫ1 ж®ӢдҪҷеә”еҠӣдҪңз”Ёж•Ҳжһң
: m' _; I2 u0 F. s: ~
2гҖҒXе°„зәҝиЎҚе°„жі•жөӢйҮҸж®ӢдҪҷеә”еҠӣзҡ„еҸ‘еұ•
5 @+ R4 U) w: {! I9 f1 C Xе°„зәҝиЎҚе°„жі•дҪңдёәдёҖз§Қж— жҚҹе®ҡйҮҸеҢ–жҜ”иҫғеҮҶзЎ®зҡ„ж®ӢдҪҷеә”еҠӣжөӢе®ҡж–№жі•пјҢе№ҝжіӣзҡ„еә”з”ЁеңЁйӣ¶д»¶еҠ е·ҘгҖҒи®ҫеӨҮеҲ¶йҖ е®үиЈ…зӯүиҙЁйҮҸжҺ§еҲ¶зҺҜиҠӮд»ҘеҸҠеӨұж•ҲеҲҶжһҗе’Ңе®үе…ЁиҜ„дј°зӯүж–№йқўпјҢеҜ№жҸҗй«ҳдә§е“ҒиҙЁйҮҸгҖҒйҳІжӯўдә§е“Ғж—©жңҹеӨұж•Ҳзӯүиө·еҲ°дәҶйқһеёёйҮҚиҰҒзҡ„дҪңз”ЁгҖӮ
- V9 w, `9 |* a( t* z9 u Xе°„зәҝжі•жҳҜз”ұдҝ„еӣҪеӯҰиҖ…дәҺ1929е№ҙжҸҗеҮәгҖӮ20дё–зәӘеҲқпјҢдәә们е°ұе·Із»ҸејҖе§ӢеҲ©з”ЁXе°„зәҝжқҘжөӢе®ҡжҷ¶дҪ“зҡ„еә”еҠӣгҖӮеҗҺжқҘж—Ҙжң¬жҲҗеҠҹи®ҫи®ЎеҮәзҡ„Xе°„зәҝеә”еҠӣжөӢе®ҡд»ӘпјҢеҜ№дәҺж®ӢдҪҷеә”еҠӣжөӢиҜ•жҠҖжңҜзҡ„еҸ‘еұ•еҒҡеҮәжқҘе·ЁеӨ§иҙЎзҢ®гҖӮ
# }3 _6 q) {/ w8 Q% d 1961е№ҙпјҢеҫ·еӣҪзҡ„E.MchearauchжҸҗеҮәдәҶXе°„зәҝеә”еҠӣжөӢе®ҡзҡ„sin2ПҲжі•пјҢдҪҝеә”еҠӣжөӢе®ҡзҡ„е®һйҷ…еә”з”Ёеҗ‘еүҚжҺЁиҝӣдәҶдёҖеӨ§жӯҘгҖӮ
" B, ^$ t- Q% b$ p9 ?* Y3 q A 然иҖҢйҒ—жҶҫзҡ„жҳҜпјҢйҡҸзқҖж®ӢдҪҷеә”еҠӣжөӢиҜ•и®ҫеӨҮеҲ¶йҖ жҠҖжңҜзҡ„еҝ«йҖҹеҸ‘еұ•пјҢиЎҢдёҡзјәд№Ҹзӣёе…іж ҮеҮҶпјҢзјәе°‘и¶іеӨҹзҡ„и®ҫеӨҮжЈҖе®ҡжҠҖжңҜдҫқжҚ®пјҢеҜјиҮҙжөӢиҜ•ж–№жі•ж— жүҖйҖӮд»ҺпјҢеҗ„е®һйӘҢе®ӨеҫҲйҡҫиҝӣиЎҢжөӢиҜ•ж•°жҚ®зҡ„жҜ”еҜ№е’ҢиғҪеҠӣйӘҢиҜҒпјҢеҫҲйҡҫе…·жңүе…¬дҝЎеҠӣгҖӮ
! D9 x8 e6 f3 V1 }8 ?* q5 H0 ?
1971е№ҙпјҢзҫҺеӣҪжұҪиҪҰе·ҘзЁӢеёҲеӯҰдјҡеҸ‘еёғ第дёҖдёӘиЎҢдёҡж ҮеҮҶSAE J784a "Residential Stress Measurement by X-ray Diffraction";
+ P+ E w' v: ~1 C: d йҡҸеҗҺ1973е№ҙпјҢж—Ҙжң¬жқҗж–ҷеӯҰдјҡйўҒеёғ第дёҖдёӘеӣҪ家ж ҮеҮҶJSMS-SD-10-73" Standard Method for X-ray Stress Measurement"гҖӮ
2 K. P: m7 V* W3 D" A
дёәеҸҚжҳ жңҖж–°зҡ„жҠҖжңҜиҝӣжӯҘе’ҢжҲҗзҶҹзҡ„жөӢиҜ•ж–№жі•пјҢ欧зӣҹж ҮеҮҶ委е‘ҳдјҡ(CEN)дәҺ2008е№ҙ7жңҲ4ж—Ҙжү№еҮҶдәҶж–°зҡ„Xе°„зәҝиЎҚе°„ж®ӢдҪҷеә”еҠӣжөӢиҜ•ж ҮеҮҶ EN 15305-2008 "Non-destructive Testing- Test Method for Residual Stress analysis by X-ray Difraction"пјҢиҜҘж ҮеҮҶдәҺ2009е№ҙ2жңҲеә•еңЁжүҖжңү欧зӣҹжҲҗе‘ҳеӣҪжӯЈејҸж–ҪиЎҢгҖӮ
2 L" K+ E# ]% r- s0 s иҜҘж ҮеҮҶеҜ№Xе°„зәҝж®ӢдҪҷеә”еҠӣжөӢиҜ•зҡ„жҠҖжңҜе’Ңж–№жі•зӯүиҜёеӨҡж–№йқўиҝӣиЎҢдәҶжӣҙж–°пјҢи§ЈеҶідәҶдёҠиҝ°зҡ„иЎҢдёҡй—®йўҳпјҢе…ЁйқўгҖҒз»ҶиҮҙзі»з»ҹйҳҗиҝ°дәҶXе°„зәҝиЎҚе°„жі•ж®ӢдҪҷеә”еҠӣеҲҶжһҗзҡ„еҺҹзҗҶгҖҒжөӢе®ҡж–№жі•гҖҒжқҗж–ҷзү№жҖ§гҖҒд»ӘеҷЁйҖүжӢ©е’Ңеёёи§Ғй—®йўҳеӨ„зҗҶзӯүж–№йқўзҡ„еҶ…е®№гҖӮж–°ж ҮеҮҶд№ҹеӣ жӯӨиҺ·еҫ—дәҶдёҡз•Ңзҡ„дёҖиҮҙи®ӨеҸҜгҖӮ
6 i' a+ ]) t2 D2 \2 o) S* O* h
дёҺд№Ӣзӣёе‘јеә”пјҢзҫҺеӣҪиҜ•йӘҢжқҗж–ҷеӯҰдјҡ(ASTM)д№ҹдәҺ2010е№ҙ7жңҲеҸ‘еёғдәҶжңҖж–°зҡ„зҫҺеӣҪж ҮеҮҶзүҲжң¬ ASTM E91510 "Standard Test Method for Verifying the Alignment of X-ray Diffraction Instrumentation for Residual Stress Measurement"гҖӮ
* W- `9 G! L J3 D+ a+ z$ X
д№ӢеҗҺпјҢ欧зҫҺеӣҪ家еӣҙз»•Xе°„зәҝиЎҚе°„жі•пјҢйўҒеёғдәҶдёҖзі»еҲ—жЈҖжөӢж ҮеҮҶпјҢдёәиЎҢдёҡеҸ‘еұ•ж ‘з«ӢдәҶж ҮжқҶпјҢXе°„зәҝиЎҢе°„жі•жөӢе®ҡж®ӢдҪҷеә”еҠӣеҫ—еҲ°дәҶи¶ҠжқҘи¶Ҡе№ҝжіӣзҡ„еә”з”ЁпјҢжҠҖжңҜжүӢж®өд№ҹж—ҘзӣҠжҲҗзҶҹгҖӮ
0 _8 i+ w' O/ d" S* x 3гҖҒXе°„зәҝиЎҚе°„жі•жөӢйҮҸж®ӢдҪҷеә”еҠӣзҡ„еҹәжң¬еҺҹзҗҶ
, E/ P9 ]/ N$ m5 v
Xе°„зәҝиЎҚе°„жөӢйҮҸж®ӢдҪҷеҶ…еә”еҠӣзҡ„еҹәжң¬еҺҹзҗҶжҳҜд»ҘжөӢйҮҸиЎҚе°„зәҝдҪҚ移дҪңдёәеҺҹе§Ӣж•°жҚ®пјҢжүҖжөӢеҫ—зҡ„з»“жһңе®һйҷ…дёҠжҳҜж®ӢдҪҷеә”еҸҳпјҢиҖҢж®ӢдҪҷеә”еҠӣжҳҜйҖҡиҝҮиғЎе…Ӣе®ҡеҫӢз”ұж®ӢдҪҷеә”еҸҳи®Ўз®—еҫ—еҲ°зҡ„гҖӮ
+ `3 Y# B8 V: ?2 h" R2 X е…¶еҹәжң¬еҺҹзҗҶжҳҜпјҡеҪ“иҜ•ж ·дёӯеӯҳеңЁж®ӢдҪҷеә”еҠӣж—¶пјҢжҷ¶йқўй—ҙи·қе°ҶеҸ‘з”ҹеҸҳеҢ–пјҢеҸ‘з”ҹеёғжӢүж јиЎҚе°„ж—¶пјҢдә§з”ҹзҡ„иЎҚе°„еі°д№ҹе°ҶйҡҸд№Ӣ移еҠЁпјҢиҖҢ且移еҠЁи·қзҰ»зҡ„еӨ§е°ҸдёҺеә”еҠӣеӨ§е°Ҹзӣёе…ігҖӮз”Ёжіўй•ҝО»зҡ„Xе°„зәҝпјҢе…ҲеҗҺж•°ж¬Ўд»ҘдёҚеҗҢзҡ„е…Ҙе°„и§’з…§е°„еҲ°иҜ•ж ·дёҠпјҢжөӢеҮәзӣёеә”зҡ„иЎҚе°„и§’2ОёпјҢжұӮеҮә2ОёеҜ№sin2ПҲзҡ„ж–ңзҺҮMпјҢдҫҝеҸҜз®—еҮәеә”еҠӣПғПҲгҖӮ
* O8 Z) ]" l9 n5 K9 u+ e5 Z Xе°„зәҝиЎҚе°„ж–№жі•дё»иҰҒжҳҜжөӢиҜ•жІҝиҜ•ж ·иЎЁйқўжҹҗдёҖж–№еҗ‘дёҠзҡ„еҶ…еә”еҠӣПғПҶгҖӮдёәжӯӨйңҖеҲ©з”Ёеј№жҖ§еҠӣеӯҰзҗҶи®әжұӮеҮәПғПҶзҡ„иЎЁиҫҫејҸгҖӮз”ұдәҺXе°„зәҝеҜ№иҜ•ж ·зҡ„з©ҝе…ҘиғҪеҠӣжңүйҷҗпјҢеҸӘиғҪжҺўжөӢиҜ•ж ·зҡ„иЎЁеұӮеә”еҠӣпјҢиҝҷз§ҚиЎЁеұӮеә”еҠӣеҲҶеёғеҸҜи§ҶдёәдәҢз»ҙеә”еҠӣзҠ¶жҖҒпјҢе…¶еһӮзӣҙиҜ•ж ·зҡ„дё»еә”еҠӣПғ3 вүҲ0(иҜҘж–№еҗ‘зҡ„дё»еә”еҸҳОө3вү 0)гҖӮ
8 F$ [8 ~7 t$ x2 L2 G% r \
з”ұжӯӨпјҢеҸҜжұӮеҫ—дёҺиҜ•ж ·иЎЁйқўжі•еҗ‘жҲҗОЁи§’зҡ„еә”еҸҳОөОЁзҡ„иЎЁиҫҫејҸдёәпјҡ
Z/ g) K1 J" v' t- @7 P3 c8 ?# @ 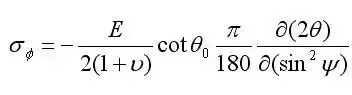
' ^( A+ v- S, ]
ОөПҲзҡ„йҮҸеҖјеҸҜд»Ҙз”ЁиЎҚе°„жҷ¶йқўй—ҙи·қзҡ„зӣёеҜ№еҸҳеҢ–жқҘиЎЁзӨәпјҢдё”дёҺиЎҚе°„еі°дҪҚ移иҒ”зі»иө·жқҘпјҢеҚіпјҡ
& g4 y" T; i% v! q: `8 P 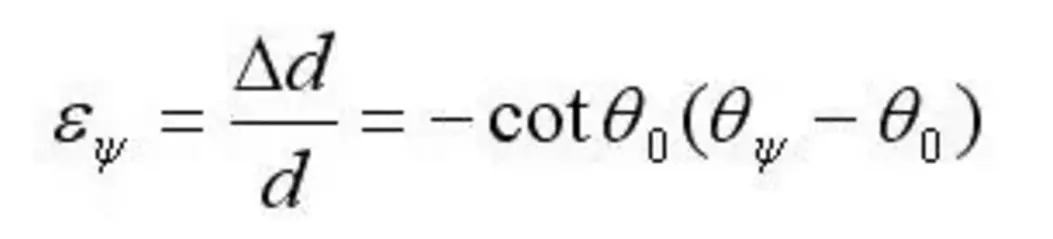
1 Z; z: `( U1 k ејҸдёӯОё0дёәж— еә”еҠӣиҜ•ж ·иЎҚе°„еі°зҡ„еёғжӢүж ји§’пјҢОёПҲдёәжңүеә”еҠӣиҜ•ж ·иЎҚе°„еі°дҪҚзҡ„еёғжӢүж ји§’гҖӮ
& _8 w( Y9 w+ d; S8 ]* [ d- j8 e
дәҺжҳҜе°ҶдёҠејҸд»Је…Ҙ并жұӮеҒҸеҜјпјҢеҸҜеҫ—пјҡ
9 B! [3 N. E7 Y, y f2 T 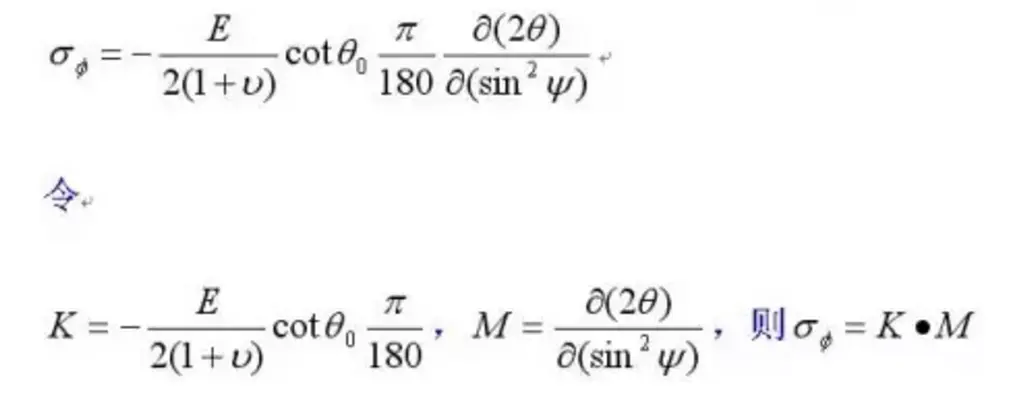
2 m# d5 e @$ Z$ {. T0 N
е…¶дёӯKжҳҜеҸӘдёҺжқҗж–ҷжң¬иҙЁгҖҒйҖүе®ҡиЎҚе°„йқўHKLжңүе…ізҡ„еёёж•°пјҢеҪ“жөӢйҮҸзҡ„ж ·е“ҒжҳҜеҗҢдёҖз§Қжқҗж–ҷпјҢиҖҢдё”йҖүе®ҡзҡ„иЎҚе°„йқўжҢҮж•°зӣёеҗҢж—¶пјҢKдёәе®ҡеҖјпјҢз§°дёәеә”еҠӣзі»ж•°гҖӮMжҳҜпјҲ2Оёпјү-sin2ПҲзӣҙзәҝзҡ„ж–ңзҺҮпјҢеҜ№еҗҢдёҖиЎҚе°„йқўHKLпјҢйҖүжӢ©дёҖз»„ПҲеҖјпјҲ0В°гҖҒ15В°гҖҒ30В°гҖҒ45В°пјүпјҢжөӢйҮҸзӣёеә”зҡ„пјҲ2ОёпјүПҲд»ҘпјҲ2Оёпјү-sin2ПҲдҪңеӣҫпјҢ并д»ҘжңҖе°ҸдәҢд№ҳжі•жұӮеҫ—ж–ңзҺҮMпјҢе°ұеҸҜи®Ўз®—еҮәеә”еҠӣ пјҲПҶжҳҜиҜ•ж ·е№ійқўеҶ…йҖүе®ҡдё»еә”еҠӣж–№еҗ‘еҗҺпјҢжөӢеҫ—зҡ„еә”еҠӣдёҺдё»еә”еҠӣж–№еҗ‘зҡ„еӨ№и§’пјүгҖӮз”ұдәҺK<0пјҢжүҖд»ҘпјҢM<0ж—¶пјҢдёәжӢүеә”еҠӣпјҢM>0ж—¶дёәеҺӢеә”еҠӣпјҢиҖҢM=0ж—¶ж— еә”еҠӣеӯҳеңЁгҖӮ
1 A3 W+ z2 L4 R& N( T
4гҖҒж ·е“ҒдёҺиЎҚе°„йқўд№Ӣй—ҙзҡ„е…ізі»
8 m. W, N H! g" \2 B$ t* F4 x
пјҲ1пјүиЎҚе°„д»ӘжөӢйҮҸжөӢйҮҸж®ӢдҪҷеә”еҠӣзҡ„е®һйӘҢж–№жі•
: [' `; z! e0 z: Y7 i' d( M% v1 L
еңЁдҪҝз”ЁиЎҚе°„д»ӘжөӢйҮҸеә”еҠӣж—¶пјҢиҜ•ж ·дёҺжҺўжөӢеҷЁОё-2Оёе…ізі»иҒ”еҠЁпјҢеұһдәҺеӣәе®ҡПҲжі•гҖӮйҖҡеёёПҲ=0В°гҖҒ15В°гҖҒ30В°гҖҒ45В°жөӢйҮҸж•°ж¬ЎгҖӮ
* z1 b6 j$ J, f) L3 |- k# V" E" S- q еҪ“ПҲ=0ж—¶пјҢдёҺ常规дҪҝз”ЁиЎҚе°„д»Әзҡ„ж–№жі•дёҖж ·пјҢе°ҶжҺўжөӢеҷЁ(и®°ж•°з®Ў)ж”ҫеңЁзҗҶи®әз®—еҮәзҡ„иЎҚе°„и§’2ОёеӨ„пјҢжӯӨж—¶е…Ҙе°„зәҝеҸҠиЎҚе°„зәҝзӣёеҜ№дәҺж ·е“ҒиЎЁйқўжі•зәҝе‘ҲеҜ№з§°ж”ҫе°„й…ҚзҪ®гҖӮ然еҗҺдҪҝиҜ•ж ·дёҺжҺўжөӢеҷЁжҢүОё-2ОёиҒ”еҠЁгҖӮеңЁ2ОёеӨ„йҷ„иҝ‘жү«жҸҸеҫ—еҮәжҢҮе®ҡзҡ„HKLиЎҚе°„зәҝзҡ„еӣҫи°ұгҖӮеҪ“ПҲвү 0ж—¶пјҢе°ҶиЎҚе°„д»ӘжөӢи§’еҸ°зҡ„Оё-2ОёиҒ”еҠЁеҲҶејҖгҖӮе…ҲдҪҝж ·е“ҒйЎәж—¶й’ҲиҪ¬иҝҮдёҖдёӘ规е®ҡзҡ„ПҲи§’еҗҺпјҢиҖҢжҺўжөӢеҷЁд»ҚеӨ„дәҺ0гҖӮ然еҗҺиҒ”дёҠОё-2ОёиҒ”еҠЁиЈ…зҪ®еңЁ2ОёеӨ„йҷ„иҝ‘иҝӣиЎҢжү«жҸҸпјҢеҫ—еҮәеҗҢдёҖжқЎHKLиЎҚе°„зәҝзҡ„еӣҫи°ұгҖӮ
8 _4 r/ B8 g8 r& X! v8 C$ U жңҖеҗҺпјҢдҪң2Оё-sin2ПҲзҡ„е…ізі»зӣҙзәҝпјҢжңҖеҗҺжҢүеә”еҠӣиЎЁиҫҫПғ=KВ·О”2Оё/О”sin2ПҲ= KВ·MжұӮеҮәеә”еҠӣеҖјгҖӮ
" V' {* k. [$ a3 V5 z* A( z пјҲ2пјүж®ӢдҪҷеҶ…еә”еҠӣжөӢиҜ•зҡ„ж•°жҚ®еӨ„зҗҶ
- p& I4 Q, a. a3 F2 D! k з”ұеёғжӢүж јж–№зЁӢеҸҜзҹҘпјҢОёи§’и¶ҠеӨ§еҲҷиө·жөӢйҮҸиҜҜе·®еј•иө·в–іпҪ„/пҪ„зҡ„иҜҜе·®и¶Ҡе°ҸпјҢжүҖд»ҘжөӢйҮҸж—¶еә”йҖүжӢ©Оёи§’е°ҪйҮҸеӨ§дәҺиЎҚе°„йқўгҖӮеҸ–nдёӘдёҚеҗҢзҡ„ПҲи§’еәҰиҝӣиЎҢжөӢе®ҡ2Оёi(i=1пјҢ2пјҢ3пјҢвҖҰпјҢn)пјҢдёҖиҲ¬еҸҜеҸ–nвүҘ4пјҢ йҮҮз”Ёж•°жҚ®еӨ„зҗҶзЁӢеәҸеҜ№2ОёОЁзҡ„еҺҹе§ӢжөӢйҮҸж•°жҚ®иҝӣиЎҢжүЈйҷӨиғҢеә•гҖҒж•°еҖје№іж»‘гҖҒзЎ®е®ҡеі°дҪҚзӯүеӨ„зҗҶеҗҺз»ҷеҮә2ОёОЁеҖјз„¶еҗҺйҮҮз”ЁжңҖе°ҸдәҢд№ҳжі•е°Ҷеҗ„ж•°жҚ®зӮ№еӣһеҪ’жҲҗзӣҙзәҝпјҡи®ҫзӣҙзәҝж–№зЁӢдёәпјҡе…¶дёӯпјҡ
8 H0 y0 Z6 e% M& F" N, I8 r
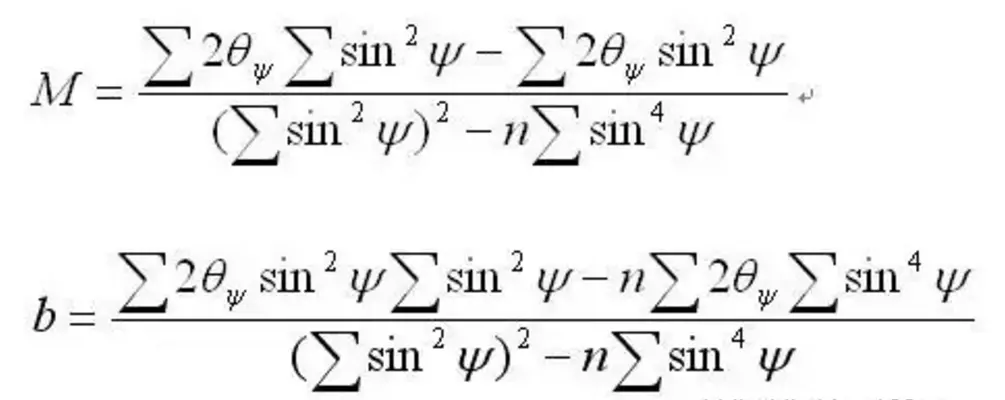
7 B0 [; l$ I, l; M ејҸдёӯnдёәжөӢйҮҸж•°жҚ®зҡ„ж•°зӣ®гҖӮз”ұдёҠејҸеҸҜжұӮеҫ—зӣҙзәҝж–ңзҺҮMгҖӮ
# @" r" t* W- W жҹҘеҮәеј№жҖ§жЁЎйҮҸEе’ҢжіҠжқҫжҜ”П…пјҢеҸҜи®Ўз®—еҮәKпјҢ然еҗҺз”ұПғ=KВ·MжұӮеҮәеә”еҠӣгҖӮ
2 X# E/ _( V: R/ L N, B+ v6 @6 h пјҲ3пјүиЎҚе°„еі°дҪҚзҡ„зЎ®е®ҡ
8 C" ~4 ^4 ~ z& y* z4 g& x
еңЁе®Ҹи§Ӯеә”еҠӣжөӢйҮҸдёӯпјҢеҮҶзЎ®ең°жөӢе®ҡиЎҚе°„еі°зҡ„дҪҚзҪ®жҳҜжһҒе…¶йҮҚиҰҒзҡ„гҖӮеёёз”Ёзҡ„е®ҡеі°ж–№жі•еҫҲеӨҡпјҢеҰӮеҚҠй«ҳе®Ҫжі•гҖҒ1/8й«ҳеәҰжі•гҖҒеі°йЎ¶жі•гҖҒеҲҮзәҝжі•зӯүпјҢдёүзӮ№жҠӣзү©зәҝжӢҹеҗҲе®ҡеі°жі•зӯүгҖӮ
" W) d& f5 J3 W) t
жңҖеёёз”Ёзҡ„жҳҜдёүзӮ№жҠӣзү©зәҝжі•пјҢиҝҷжҳҜдёҖз§ҚиҫғдёәзІҫзЎ®иҖҢдёҚиҝҮдәҺз№ҒжқӮзҡ„е®ҡеі°дҪҚжі•гҖӮеҚіпјҡеңЁиЎҚе°„еі°йЎ¶йҷ„иҝ‘еҸ–д»Ҙзӯүи§’еәҰй—ҙйҡ”О”2ОёеҲҶејҖзҡ„дёүдёӘж•°жҚ®зӮ№пјҢжұӮеҫ—е…¶жҠӣзү©зәҝйЎ¶зӮ№гҖӮ
9 n7 R3 G b) N3 _. j& ~/ z! V+ v еҲ©з”ЁMDI JadeпјҢзЎ®е®ҡеі°дҪҚзҡ„ж–№жі•еҫҲеӨҡгҖӮеҜ»еі°жҳҜжңҖз®ҖеҚ•зҡ„еі°дҪҚзЎ®е®ҡж–№жі•пјҢеҜ»еі°жҠҘе‘ҠдёӯжҳҫзӨәдәҶиЎҚе°„еі°зҡ„еі°дҪҚгҖҒејәеәҰзӯүзӣёе…ізҡ„ж•°жҚ®пјӣи®Ўз®—еі°йқўз§Ҝе‘Ҫд»Өд№ҹдёҚеӨұдёәдёҖз§ҚеҘҪзҡ„ж–№жі•пјҢеі°дҪҚзІҫзЎ®жҖ§еә”еңЁеҜ»еі°ж–№жі•д№ӢдёҠпјӣ第дёүз§Қж–№жі•е°ұжҳҜеҜ№еі°иҝӣиЎҢжӢҹеҗҲпјҢйҖҡеёёйҮҮз”ЁжҠӣзү©зәҝжӢҹеҗҲж–№жі•пјҢжӢҹеҗҲж—¶дёҚйңҖиҰҒжүЈйҷӨиғҢжҷҜе’ҢKОұ2пјҢJadeдјҡиҮӘеҠЁжүЈйҷӨе…¶еҪұе“ҚпјҢдҪҶйңҖиҰҒйҖӮеҪ“е№іж»‘гҖӮеҸҰеӨ–пјҢJADE6.5дёӯжңүеә”еҠӣи®Ўз®—еҠҹиғҪпјҢдҪҶеҸ‘зҺ°JADE5ж— жӯӨеҠҹиғҪпјҢдҪҶеҸҜд»ҘиҝӣиЎҢеі°зҡ„жӢҹеҗҲгҖӮ
9 o# [5 E1 I. D- `) j7 k е…¶е®ғиҪҜ件д№ҹеҸҜд»Ҙе®ҢжҲҗеі°зҡ„жӢҹеҗҲпјҢи®Ўз®—еҮәеі°зҡ„дҪҚзҪ®гҖӮ
" U p3 \+ j3 d8 s
5гҖҒз”Ёпјёе°„зәҝжі•жөӢе®ҡеә”еҠӣдёӯеӯҳеңЁзҡ„й—®йўҳ
4 F5 D5 y7 b2 z' T+ x еңЁе№ійқўеә”еҠӣзҡ„еҒҮе®ҡдёӢпјҢз”ұ2Оё-sin2ПҲзӣҙзәҝзҡ„ж–ңзҺҮжқҘжұӮжөӢе®Ҹи§Ӯеә”еҠӣпјҢжҳҜ常规зҡ„еә”еҠӣжөӢе®ҡж–№жі•гҖӮдҪҶеңЁжөӢйҮҸдёӯеҫҖеҫҖеҸ‘зҺ°е…¶2Оё-sin2ПҲе…ізі»еҒҸзҰ»зәҝжҖ§пјҢе‘ҲжӣІзәҝгҖҒеҲҶиЈӮжҲ–жіўеҠЁзҺ°иұЎпјҢиҝҷиЎЁжҳҺеңЁжқҗж–ҷдёӯеӯҳеңЁеә”еҠӣжўҜеәҰгҖҒеһӮзӣҙиЎЁйқўзҡ„еҲҮеә”еҠӣжҲ–з»Үжһ„гҖӮвҖңПҲеҲҶиЈӮвҖқжҳҜжҢҮеңЁПҲе’Ң-ПҲж–№еҗ‘жөӢе®ҡеҫ—еҲ°дёҚеҗҢзҡ„2Оё(Оө)еҖјпјҢдҪҝ2Оё-sin2ПҲжӣІзәҝеҲҶжҲҗдёӨж”ҜгҖӮжҲ‘们зҹҘйҒ“пјҢиҝҷжҳҜеһӮзӣҙдәҺиЎЁйқўзҡ„еҲҮеә”еҠӣПғ13гҖҒПғ23вү 0зҡ„з»“жһңгҖӮеҜ№жӯӨй—®йўҳзҡ„зІ—з•ҘеӨ„зҗҶжҳҜеҸ–ВұПҲжөӢйҮҸеҖјзҡ„е№іеқҮпјҢи®Ўз®—е№іеқҮзҡ„еә”еҠӣеҖјгҖӮеңЁеә”еҠӣзҡ„пјёе°„зәҝжөӢе®ҡдёӯпјҢиҝҳеҸҜиғҪеӯҳеңЁ2Оё-sin2ПҲе…ізі»зҡ„вҖңжҢҜиҚЎвҖқзҺ°иұЎпјҢиЎЁжҳҺжқҗж–ҷдёӯеӯҳеңЁжҳҺжҳҫзҡ„з»Үжһ„гҖӮеңЁе®һйӘҢиҝҮзЁӢдёӯеҸҜйҖүз”Ёй«ҳиЎҚе°„и§’пјҢдҪҺеҜ№з§°жҖ§зҡ„й«ҳжҢҮж•°иЎҚе°„йқўиЎҚе°„зәҝпјҢиҝҷж ·зҡ„иЎҚе°„зәҝиҫғе°‘еҸ—з»Үжһ„зҡ„еҪұе“ҚгҖӮ
$ L9 T9 |. z& T3 P
6гҖҒж®ӢдҪҷеә”еҠӣжөӢйҮҸе®һйӘҢж–№жі•зҡ„еҸ‘еұ•
& h8 Y X" ~4 y# p( ~+ `- |; j
Xе°„зәҝзҡ„з©ҝйҖҸж·ұеәҰиҫғе°ҸпјҢеҸӘиғҪжөӢйҮҸжқҗж–ҷиЎЁйқўзҡ„ж®ӢдҪҷеә”еҠӣпјҢеҰӮжһңйңҖиҰҒжөӢйҮҸжқҗж–ҷеҶ…йғЁзҡ„ж®ӢдҪҷеә”еҠӣпјҢжҲ–иҖ…жөӢйҮҸеә”еҠӣжўҜеәҰпјҢе…¶иғҪеҠӣеҲҷжҳҫеҫ—жңүдәӣиӢҚзҷҪгҖӮйҖҡеёёи§ЈеҶізҡ„еҠһжі•жҳҜйңҖиҰҒйҮҮз”ЁеүҘеұӮжі•гҖӮеҚіеҜ№ж ·е“ҒйҖҗеұӮеүҘзҰ»пјҢжөӢйҮҸжҜҸеұӮиЎЁйқўзҡ„еә”еҠӣпјҢ然еҗҺйҮҮз”ЁдёҖе®ҡзҡ„з®—жі•жүЈйҷӨеӣ дёәеүҘеұӮйҖ жҲҗзҡ„еә”еҠӣжқҫејӣпјҢжҚўз®—жҲҗеҗ„еұӮзңҹе®һзҡ„еә”еҠӣгҖӮ
: T2 E# S& ^& d7 B иҝ‘е№ҙжқҘпјҢжңүдәәйҮҮз”ЁдёӯеӯҗиЎҚе°„жі•е’ҢеҗҢжӯҘиҫҗе°„Xе°„зәҝйҖҸиҝҮжі•жқҘжөӢйҮҸжқҗж–ҷж·ұеәҰзҡ„ж®ӢдҪҷеә”еҠӣгҖӮ
0 } a" g2 W" ]1 u
дёӯеӯҗиЎҚе°„жі•жҳҜдёҖз§ҚжөӢйҮҸз»“жһ„еҶ…йғЁеә”еҠӣзҡ„еёёз”Ёж–№жі•гҖӮдёӯеӯҗиЎҚе°„жі•д»ҘдёӯеӯҗжөҒдёәе…Ҙе°„жқҹпјҢз…§е°„иҜ•ж ·пјҢеҪ“жҷ¶йқўз¬ҰеҗҲеёғжӢүж јжқЎд»¶ж—¶пјҢдә§з”ҹиЎҚе°„пјҢеҫ—еҲ°иЎҚе°„еі°гҖӮиҜҘж–№жі•зҡ„еҺҹзҗҶдёҺжҷ®йҖҡXе°„зәҝиЎҚе°„ж–№жі•зұ»дјјпјҢд№ҹжҳҜж №жҚ®иЎҚе°„еі°дҪҚзҪ®зҡ„еҸҳеҢ–пјҢжұӮеҮәеә”еҠӣгҖӮдҪҶдёҺжҷ®йҖҡXе°„зәҝиЎҚе°„жі•зӣёжҜ”пјҢдёӯеӯҗиЎҚе°„жі•еҲ©з”ЁдёӯеӯҗиғҪз©ҝйҖҸиҜ•ж ·иҫғеӨ§ж·ұеәҰзҡ„зү№жҖ§пјҢеҸҜд»ҘжөӢеҫ—ж ·е“ҒеҶ…йғЁж®ӢдҪҷеә”еҠӣпјҢдё”йҖӮдәҺеҜ№еӨ§еқ—иҜ•ж ·иҝӣиЎҢжөӢе®ҡгҖӮеӣ жӯӨпјҢдёӯеӯҗиЎҚе°„жі•еҜ№жөӢе®ҡж ·е“ҒеҶ…йғЁе№іеқҮж®ӢдҪҷеә”еҠӣе…·жңүеҫҲеӨ§зҡ„дјҳи¶ҠжҖ§гҖӮ
5 j; f- K! Q b0 t; {5 J
еӣ дёәеҗҢжӯҘиҫҗе°„Xе°„зәҝзҡ„ејәеәҰй«ҳеҸҜд»ҘйҖҸиҝҮж ·е“ҒпјҢеӣҪеӨ–е·ІжңүеӯҰиҖ…йҮҮз”ЁйҖҸиҝҮжі•жөӢйҮҸйҮ‘еҲҡзҹідёҺзЎ¬иҙЁеҗҲйҮ‘еӨҚеҗҲеұӮзҡ„еҶ…йғЁж®ӢдҪҷеә”еҠӣгҖӮ
) w! u* F i) O 7гҖҒж®ӢдҪҷеә”еҠӣи®Ўз®—иҪҜ件зҡ„дҪҝз”Ё
* U/ }' ?! D7 n* s& m* Q пјҲ1пјүж•°жҚ®жөӢйҮҸ
- u) T: w& {% [
е…ҲеҜ№ж ·е“ҒдҪңдёҖдёӘ70-140В°иҢғеӣҙеҶ…зҡ„жү«жҸҸпјҢи§ӮеҜҹж ·е“Ғзҡ„иЎҚе°„еі°жғ…еҶөпјҢйҖүжӢ©дёҖдёӘејәеәҰиҫғй«ҳпјҢдёҚжј«ж•ЈпјҢиЎҚе°„йқўжҢҮж•°иҫғй«ҳзҡ„иЎҚе°„еі°дҪңдёәз ”з©¶еҜ№иұЎеі°гҖӮжҢүз…§ж®ӢдҪҷеә”еҠӣжөӢйҮҸзҡ„иҰҒжұӮпјҢи®ҫзҪ®дёҚеҗҢзҡ„ПҲпјҲ0В°пјҢ15В°пјҢ30В°пјҢ45В°пјүи§’пјҢд»Ҙж…ўйҖҹжү«жҸҸж–№ејҸжөӢйҮҸдёҚеҗҢПҲи§’дёӢзҡ„еҚ•еі°иЎҚе°„и°ұгҖӮжҜҸдёӘПҲи§’зҡ„жөӢйҮҸж•°жҚ®дҝқеӯҳдёәдёҖдёӘж–Ү件пјҢеҰӮ00пјҢ10пјҢ20пјҢ30пјҢ40зӯүгҖӮ
9 T! T" ~. K) q/ ^
еҖјеҫ—жіЁж„Ҹзҡ„жҳҜпјҢйҖҡеёёй«ҳи§’еәҰиЎҚе°„еі°йғҪжҳҜеҫҲжј«ж•Јзҡ„пјҢеҜ№зІҫзЎ®ең°зЎ®е®ҡеі°дҪҚжңүеӣ°йҡҫпјҢдҪҶжҳҜпјҢеҰӮжһңжүҖйҖүиЎҚе°„еі°зҡ„и§’еәҰеӨӘдҪҺпјҢеңЁПҲ=45В°ж—¶пјҢеҸҜиғҪдёҚеҮәзҺ°иЎҚе°„еі°жҲ–иҖ…еі°ејәжһҒдҪҺиҖҢжј«ж•ЈпјҢеҗҢж ·еёҰжқҘи®Ўз®—иҜҜе·®гҖӮиҝҷж—¶еҸӘиғҪйҖүжӢ©ПҲиҫғе°Ҹзҡ„ж•°жҚ®пјҢеҰӮПҲ=0В°пјҢ10В°пјҢ20В°пјҢ30В°пјҢ40В°пјү并且е°ҪйҮҸең°еӨҡйҖүжӢ©еҮ дёӘПҲи§’жқҘжөӢйҮҸпјҢдҪҝе®һйӘҢж•°жҚ®жӣҙеҠ еҜҶйӣҶпјҢеҮҸе°Ҹе®һйӘҢиҜҜе·®пјҢиҝҳжңүе°ұжҳҜйҖүжӢ©ПҲи§’ж—¶пјҢе°ҪйҮҸдҪҝsin2ПҲеҸ–зӮ№еқҮеҢҖиҖҢдёҚжҳҜйҖүжӢ©ПҲзҡ„еҸ–еҖјеқҮеҢҖпјҢеӣ дёәПҲ-sin2ПҲдёҚе‘ҲзәҝжҖ§е…ізі»гҖӮ
4 S6 J3 L- G/ G9 e- V пјҲ2пјүзЎ®е®ҡеі°дҪҚ
0 e# Q @3 P: d3 P4 t% V жң¬иҪҜ件еҸҜд»ҘжҺҘеҸ—еӨҡз§Қж–№ејҸи®Ўз®—еҮәжқҘзҡ„жӢҹе°„еі°дҪҚж•°жҚ®гҖӮеҰӮй”®зӣҳиҫ“е…ҘпјҢиҜ»жӢҹеҗҲж–Ү件зӯүгҖӮ
3 R; Y$ k a& o6 F пјҲ3пјүиҫ“е…Ҙеі°дҪҚ
- J8 y/ ~' ^ v$ E& ^% q) `7 S2 v
жү“ејҖиҪҜ件пјҢиҫ“е…Ҙеі°дҪҚж•°жҚ®гҖӮ
. B% u# H5 R6 D: d$ w$ u8 d( j пјҲ4пјүи®Ўз®—sin2ПҲ
b0 R: v: U7 T, l* _- n ж №жҚ®жөӢйҮҸдҪҝз”Ёзҡ„ПҲи§’пјҢйҮҚж–°и®Ўз®—зӘ—еҸЈдёӯзҡ„sin2ПҲ
8 N& f0 B0 Z" Q: H! z# t0 }, \ пјҲ5пјүз»ҳеӣҫ-и®Ўз®—MгҖҒж ҮжіЁ
9 U) e. r# m" m; I1 ^+ r4 e
жҢүзӘ—еҸЈдёӯзҡ„жҢүй’®жҺ’еҲ—йЎәеәҸпјҢе…Ҳз»ҳеӣҫпјҢ然еҗҺи®Ўз®—зӣҙзәҝж–ңзҺҮMпјҢеҰӮжһңйңҖиҰҒпјҢд№ҹеҸҜд»Ҙж ҮжіЁж•°жҚ®гҖӮ
2 p( \9 q* w! W R7 `; J3 n пјҲ6пјүи®Ўз®—еә”еҠӣ
4 ?# Y4 P' j( o+ w
е…ҲиҰҒж №жҚ®жқҗж–ҷдёҚеҗҢпјҢжҹҘйҳ…ж–ҮзҢ®пјҢиҺ·еҫ—жүҖжөӢзү©зӣёзҡ„еј№жҖ§жЁЎйҮҸе’ҢжіҠжқҫжҜ”并иҫ“е…ҘеҲ°зӘ—еҸЈдёӯзӣёеә”зҡ„ж–Үжң¬жЎҶдёӯгҖӮ
$ ?8 V1 l# m' n$ {1 F
жҢүдёӢи®Ўз®—еә”еҠӣпјҢеә”еҠӣеёёж•°KеҖјгҖҒеә”еҠӣеҖје°ұжҳҫзӨәеңЁзӘ—еҸЈдёӯзҡ„ж–Үжң¬жЎҶдёӯгҖӮ
3 l5 c" K8 l5 ?* ^, `& H 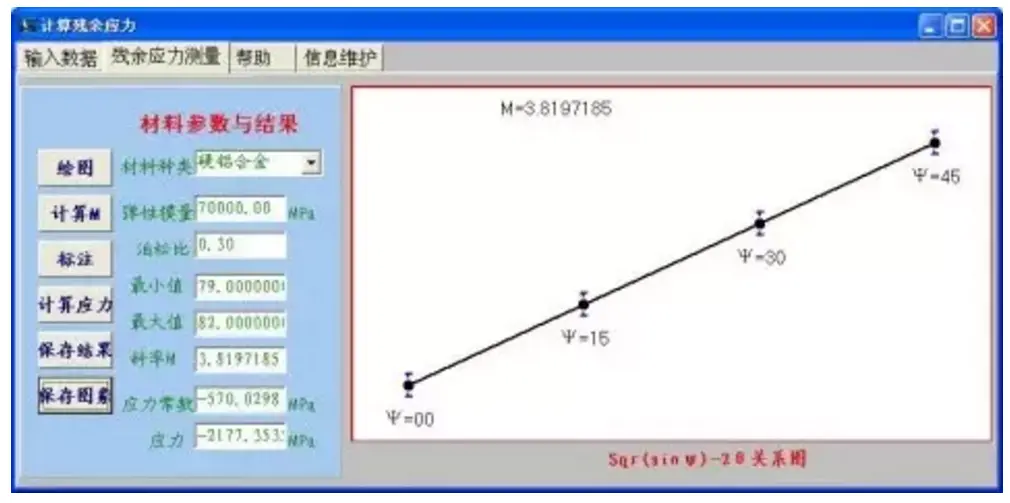
+ L! l; U8 k2 h) W& _5 f& O
пјҲ7пјүдҝқеӯҳ
4 R1 s) k) |% ~ f: T: P6 \; m
вҖңдҝқеӯҳз»“жһңвҖқ--дҝқеӯҳз»“жһңдёәж–Үжң¬ж–Ү件гҖӮ
u5 |. }. M, `4 }; \ вҖңдҝқеӯҳеӣҫиұЎвҖқ--дҝқеӯҳз»“жһңдёәеӣҫзүҮж–Ү件гҖӮ
7 ?0 v% I9 p% X. Z% `, ^ дәҶи§ЈжӣҙеӨҡж®ӢдҪҷеә”еҠӣе№Іиҙ§пјҢжҗңзҙўе№¶е…іжіЁе…¬дј—еҸ·вҖңеә”еҠӣдёҺеҸҳеҪўжҺ§еҲ¶вҖқпјҢжҜҸе‘Ёжӣҙж–°гҖӮ
: h3 j7 `5 f+ ]7 x" u


