1 P7 E, @% d. | 一直做地理 所以最专业
: C3 E% ]; y, q9 I
最强的地理自媒体科普矩阵
6 x! M4 y( r: g$ i
地球半径是指从地球中心到其表面(平均海平面)的距离。
3 P" X' G) Q& l+ R/ r, Y* w7 _+ t" N" [ d 地球不是一个规则的物体。首先,它不是正球体,而是椭球体,准确地说是一个两极稍扁,赤道略鼓的扁球体; 其次,地球的南极、北极也不对称,就海平面来说,北极稍凸,南极略凹;第三,地球的外部地形起伏多变(这对测量地球半径是有影响的)。平均大约3959英里(6371.393千米)
d) ^; W6 k' E2 ]' k5 ?$ N% |# h 由于地球的自转、内部密度的不均匀以及外部的潮汐力使得地球的形状偏离球形。同时局部的地势增大了这种不均匀性,使得地球的表面状况极度复杂。为了便于处理,对地球表面的描述必须比实际更加简单。因此我们建立一个能够满足需要的地球表面的最简模型。
6 `" l+ i: l/ h4 n, G- C 所有这些常用的模型都会涉及到“半径”的概念。严格地说,立体图形中只有球体才有半径的概念,但在很多领域,包括处理地球的模型,都会扩展“半径”的用法。以下是按照精确度降序的地球模型:
1 d( N5 z7 j1 \# m7 c 地球的真实表面;
- |4 m' C, d$ ^
按照真实表面每点的平均海平面定义的大地水准面;
! P1 D0 \3 W3 `; r! y* M9 _% }9 L
对于大地水准面和椭球体来说,模型上任何一点到指定中心的确定距离被称为“地球的一条半径”或“在某点地球的半径”。同时也常用球体模型的“平均半径”来作为“地球半径”。另一方面,对应地球真实表面的“半径”是没有实际用处的。相反,相对于海平面的海拔才是有实际用途的。
( P! V4 Z$ v5 D: m5 v8 r
地球的任何一条半径长度都落在最小的约为6,357km的极半径以及最大的约为6,378km的赤道半径之间。因此地球形状与标准球体的偏差只有约三百分之一,这在大多数情况下可以充分地把地球看做球体并使用术语“地球半径”。这个概念也可以推广到其他主要的行星上去,只不过扁率有差异而已。
0 L; x* A' o$ e% X. w/ P- q 极半径
) Y* I9 J" [, t0 _
从地心到北极或南极的距离,大约3950英里(6356.9088千米)(两极的差极小,可以忽略)。
1 T$ F- I' s1 ~' w& j* } 赤道半径
0 x K, e8 i8 I
是从地心到赤道的距离,大约3963英里(6377.830千米)。
3 `1 v* G% j' u6 a 平均半径
$ \0 E" p- l/ e/ W 大约3959英里(6371.393千米) 。这个数字是地心到地球表面所有各点距离的平均值。
3 l( y' V! [* v- J' y3 g
可以这样求:平均半径=(赤道半径×2+极半径)/3
5 F+ z5 N4 F6 c" A 地球半径有时被使用作为距离单位, 特别是在天文学和地质学中常用。它通常用RE表示。
; o- `3 `, _; D. }; G! \2 F* Z
地球大概半径6370.856千米。
( [2 s- ` `: R( D: V: Q9 `& l# w
我们知道,地球的形状近似一个球形,那么怎样测出它的半径呢?据说公元前三世纪时希腊天文学家厄拉多塞内斯(Eratosthenes,公元前276—194)首次测出了地球的半径。
" R7 K, }8 C) W
他发现夏至这一天,当太阳直射到赛伊城(今埃及阿斯旺城)的水井S时,在亚历山大城的一点A的天顶与太阳的夹角为7.2°(天顶就是铅垂线向上无限延长与天空“天球”相交的一点)。他认为这两地在同一条子午线上,从而这两地间的弧所对的圆心角SOA就是7.2°(如图1)。又知商队旅行时测得A、S间的距离约为5000古希腊里,他按照弧长与圆心角的关系,算出了地球的半径约为4000古希腊里。一般认为1古希腊里约为158.5米,那么他测得地球的半径约为6340公里。
0 \3 y: H8 Q/ w" k: ^ p 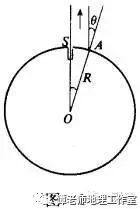
* k" T2 B* {4 ]& j& X! I 其原理为:
2 s/ ^$ x( \9 Q+ p5 ^) |
设圆周长为C,半径为R,两地间的的弧长为L,对应的圆心角为n°。
& g, e3 }3 z } V" |, O* X
因为360°的圆心角所对的弧长就是圆周长C=2πR,所以1°的圆心角所对弧长是
" L+ B3 u8 W' m$ F# [! j% K& i2 e 
/ |* f/ O# d' z, I1 V# l$ L
,即
0 d6 S( K( G9 n 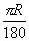
# q/ @# }1 y3 u& V6 r$ T
。于是半径为的R的圆中,n°的圆心角所对的弧长L为:
! q. i6 `2 x& l1 b7 y0 Z* B
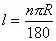
' \# ^8 [! B$ E* A7 w
。
1 U! \: U$ ?. e4 | 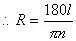
9 w ^9 T' ]! w3 }( i
。
$ a6 `0 E+ ]1 g# K$ L: p 当L=5000古希腊里,n=7.2时,
* }' [9 ~) u8 o& }! i* _
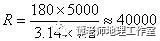
, u- g4 D+ v: A$ S7 [5 P% s 古希腊里) 化为公里数为:
3 d: ?7 a; x4 ~% r: }! Q

! f1 w0 C- U% L% z x/ | (公里)。
5 C6 D7 Q; R: a3 t/ {6 j 厄拉多塞内斯这种测地球的方法常称为弧度测量法。用这种方法测量时,只要测出两地间的弧长和圆心角,就可求出地球的半径了。
# [7 v6 n8 X0 O1 @6 y5 T. g& L 近代测量地球的半径,还用弧度测量的方法,只是在求相距很远的两地间的距离时,采用了布设三角网的方法。比如求M、N两地的距离时,可以像图2那样布设三角点,用经纬仪测量出△AMB,△ABC,△BCD,△CDE,△EDN的各个内角的度数,再量出M点附近的那条基线MA的长,最后即可算出MN的长度了。
' V% R1 n+ @$ |
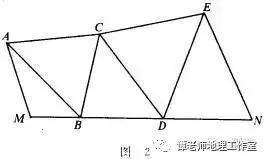
5 s e( l+ D0 c) E 通过这些三角形,怎样算出MN的长度呢?这里要用到三角形的一个很重要的定理——正弦定理。
- S3 {. k% ^$ W* R3 E9 a
即:在一个三角形中,各边和它所对角的正弦的比相等。就是说,在△ABC中,有
: ^# k7 O, ~4 [ T. `- _" i 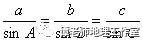
s k6 C! a! j" d2 q3 B9 v
。
" s: U; d1 R+ g# ]+ N- n L6 t5 g; G 在图2中,由于各三角形的内角已测出,AM的长也量出,由正弦定理即可分别算出:
" c+ ]) }- @/ Q# Y* p( }
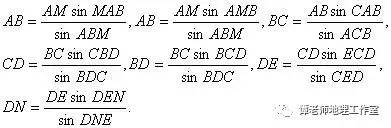
4 u( N8 W# N0 e5 R/ l' F, f' s
∴MN=MB+BD+DN。
2 x/ S. X# H( s 如果M、N两地在同一条子午线上,用天文方法测出各地的纬度后,即可算出子午线1°的长度。法国的皮卡尔(Pi-card.J.1620—1682)于1669—1671年率领他的测量队首次测出了巴黎和亚眠之间的子午线的长,求得子午线1°的长约为111.28公里,这样他推算出地球的半径约为6376公里。
( g6 u: N x/ V0 i( O# C7 H 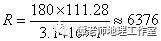
' K- k- O. K4 v5 v
(公里)。
( c. X/ W( ]8 g# `$ I/ J
另外,布设三角网有多种方法,要根据实际情况,布设的网点越少越好。
/ @: K$ l# x b0 }; s/ X* ?. { 随着科学的发展,人们对地球的认识也越来越深入,并发现地球不完全是球形的,而是一个椭球体(如图3)。科学家家们还找到了求得地球的长半径a和短半径b的方法,由于比较复杂,我们这里就不介绍了,有兴趣的同学可阅读有关书籍。
6 Z! \" J& ^8 \# ?
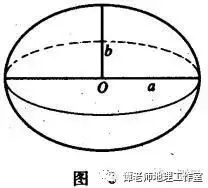
$ _: ]9 H3 O6 ^% s3 y- L$ @" T- C
你相信吗,仅仅利用一张日落的照片,你就能得出地球的半径大小! Princeton 大学的 Robert Vanderbei 在最近的一篇论文中对一张摄于密歇根湖的日落照片进行了分析,不但证实了地球是圆的,还依据照片上的内容对地球半径进行了估算。
4 ]" A! Z5 X2 j4 {' f, M 
& U3 [( W; S# [, U1 g# Y3 Q c
事情的起因就是上面这张很平常的日落照片,以及这样一个大家平时并没有太在意的问题:太阳露出水面的部分应该是一个标准的弓形,但为什么在日出日落时,我们所看到的太阳是一个橄榄球一样的形状?大家或许会很快想到,发光体的下半部分其实是日光反射在水面上造成的。随之产生的是另一个问题:为什么它的下半部分要比上半部分小一些呢?
5 |3 @$ q/ G! D- j5 r

' |/ T6 B0 V, U" r% d6 J 这是因为——想到这个问题的答案并不容易——地球是圆的。上图就是人站在地球上看日出的一个比例夸张版示意图,其中 O 为地球的中心, A 为人眼的位置, AB 为视平线, B 点为水天交界处。由于太阳距离我们相当遥远,因此我们把太阳光看作是一束理想的平行光线。我们把直接射入人眼的太阳光与 AB 的夹角记为 α ,把经过水面上的一点 C 反射进入人眼的光线与 AB 的夹角记为 β 。从图上可见,视角 β 比 α 小,也就是说太阳在水面上的镜像比本身要小一些。
, w/ b' e( J5 g$ p- n$ B

m) Q, P1 d r& }% D
β 究竟比 α 小多少呢?对照片进行精确地测量,可知太阳的直径相当于照片中的 317 个像素,而露出水面的部分高 69 像素,水中的倒影则只有 29 像素。众所周知太阳的视直径(看太阳的视角)为 0.5 度,因此我们就得到 α = 0.5 * 69 / 317 ≈ 0.1088 度, β = 0.5 * 29 / 317 ≈ 0.0457 度。
6 B- m. s4 a) H* ^6 C/ n3 t1 i 如果再已知人眼(或者说相机)离水面的垂直距离 h 为 2 米,那么根据这些数据我们就足以估算出地球的半径了。不妨把 ∠AOB 记为 φ ,把 ∠AOC 记为 θ ,把人眼到水天相接处的距离 AB 记为 D ,把人眼到反射点的距离 AC 记为 d ,入射角和反射角记为 γ ,最后用 r 来表示地球半径,那么此时我们一共有 6 个未知量。为了求解出这 6 个未知数,我们需要寻找 6 个不同的方程。这 6 个方程可以由以下 6 组等量关系得到:
; U7 ]" Q& b& _& S* Q& @ 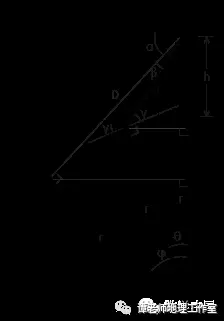
+ l" N4 W$ k6 D8 P! _ 1. 四边形 OBAC 的内角和为 360° ,即 (φ - θ) + 90° + β + (180° - γ + 90°) = 360° , 化简得 方程(1) φ + β = θ + γ
# ^. M" ?1 c2 Z" `+ Z8 @ 2. 两条平行线的同旁内角相加为 180° ,即 (α + β) + (180° - 2γ) = 180° ,即 方程(2) α + β = 2γ
G: Y8 y$ w7 I5 w8 k2 M3 M
3. 由于 AO = h + r ,同时又有 AO = AD + DO = D·sinφ + r·cosφ ,因此有 方程(3) h + r = D·sinφ + r·cosφ
% W& V1 P2 c5 v8 f. { 4. BD 既可以等于 D·cosφ ,又可以等于 r·sinφ ,于是有 方程(4) D·cosφ = r·sinφ
3 a4 T. z: f$ T/ S+ w
5. 由于 AO = h + r ,同时又有 AO = AE + EO = d·sin(γ+θ) + r·cosθ ,因此有 方程(5) h + r = d·sin(γ+θ) + r·cosθ
* s9 F7 A, |' j, k
6. CE 既可以等于 d·cos(γ+θ) ,又可以等于 r·sinθ ,于是有 方程(6) d·cos(γ+θ) = r·sinθ
! [/ Y; S; q7 V* ~0 D* k2 U 一系列复杂的代数运算(省略数百字)最终告诉我们:
7 E( s. w ~+ u& _& q* S r = h / (√1 - 2·cosβ·cosγ + cos2γ / sinβ - 1)
* }7 F+ E- C7 E# ?) b# O 其中 γ = (α + β)/2 。代入已知的 α 、 β 和 h 可以得到,地球半径 r 大约为 7.29312 * 106 米,也即 7293 千米。
3 V, v- r1 I$ o& N, [. u$ E
这个估算的误差有多大呢?事实上,地球的半径大约为 6300 多千米,可见误差不是一般的大。不过,考虑到我们估算的依据仅仅是一张照片,能把数量级估对就已经相当牛 B 了。除了测量的精度之外,还有很多潜在的因素会导致误差。目前看来,误差的最主要来源似乎是不完全平静的水面——一点小小的波浪就会给 α 、 β 的值带来巨大的影响。
' o. s/ c% D4 S* g( a

9 e% q; q: ]6 h% x. A; @- N 公元前3 世纪,古希腊天文学家埃拉托色尼首次测量出了地球的半径。他发现夏至这一天,当太阳直射到赛因域(今埃及阿斯旺城附近)的水井时,在亚历山大城的一点的天顶与太阳的夹角为7.2°。他认为这两地在同一条子午线上,从而这两地间的弧所对的圆心角就是7.2°。又知商队旅行时测得两地间的距离约为5000 古希腊里,他按照弧长与圆心角的关系,算出了地球的半径约为40 000 古希腊里。
4 ]! W$ @& Q( a- f 他是怎么算的呢?我们不妨跟古希腊人一起来做道数学题:假设圆周长为C,半径为r,两地间的弧长为l,对应的圆心角为θ。因为360°的圆心角所对的弧长是圆周长C=2πr,所以1°的圆心角所对应的弧长长度是2πr / 360,即πr / 180。于是,半径为r 的圆中,圆心角θ所对的弧长l 为:l=θπr / 180。所以,r=180 l / (θπ)。
1 N1 P& A6 J/ o% K/ q; g! ?4 h 当两地距离l 为5000 古希腊里,θ等于7.2 °时, 就算出地球半径r 是180×5000/(7.2×3.141 59 ) ≈ 40 000 古希腊里。曾有人考证,1 古希腊里约为现在的158 米,按这个关系换算,40 000 古希腊里则相当于现在的6300 千米。
% x, @- X7 X% u3 ^& g1 S1 j" T8 j
这种测地球的方法常称为弧度测量法。用这种方法测量时,只要测出两地间的弧长和圆心角,就可求出地球的半径了。
0 ]% G& H& q1 G. B0 S$ ~# T 现代测量地球的半径,还是用弧度测量的方法,法国的皮卡尔于1669—1671 年率领测量队首次测出了巴黎附近子午线1°的长约为111.28千米,从而推算出地球的半径约为6376 千米。
/ ?" U5 K# X7 V! ~' Y3 j


