, t' D2 ~5 T' {5 @! s
дёҖзӣҙеҒҡең°зҗҶ жүҖд»ҘжңҖдё“дёҡ
- I* Y( L* Z1 c4 h+ k+ J жңҖејәзҡ„ең°зҗҶиҮӘеӘ’дҪ“科жҷ®зҹ©йҳө
: c! o6 O; b b! h: f. { ең°зҗғеҚҠеҫ„жҳҜжҢҮд»Һең°зҗғдёӯеҝғеҲ°е…¶иЎЁйқў(е№іеқҮжө·е№ійқў)зҡ„и·қзҰ»гҖӮ
7 o/ t3 F8 x. z4 ? N3 R6 { ең°зҗғдёҚжҳҜдёҖдёӘ规еҲҷзҡ„зү©дҪ“гҖӮйҰ–е…ҲпјҢе®ғдёҚжҳҜжӯЈзҗғдҪ“пјҢиҖҢжҳҜжӨӯзҗғдҪ“пјҢеҮҶзЎ®ең°иҜҙжҳҜдёҖдёӘдёӨжһҒзЁҚжүҒпјҢиөӨйҒ“з•Ҙйј“зҡ„жүҒзҗғдҪ“; е…¶ж¬ЎпјҢең°зҗғзҡ„еҚ—жһҒгҖҒеҢ—жһҒд№ҹдёҚеҜ№з§°пјҢе°ұжө·е№ійқўжқҘиҜҙпјҢеҢ—жһҒзЁҚеҮёпјҢеҚ—жһҒз•ҘеҮ№;第дёүпјҢең°зҗғзҡ„еӨ–йғЁең°еҪўиө·дјҸеӨҡеҸҳ(иҝҷеҜ№жөӢйҮҸең°зҗғеҚҠеҫ„жҳҜжңүеҪұе“Қзҡ„)гҖӮе№іеқҮеӨ§зәҰ3959иӢұйҮҢ(6371.393еҚғзұі)
4 T; k* [1 U4 @* z5 _$ Z з”ұдәҺең°зҗғзҡ„иҮӘиҪ¬гҖҒеҶ…йғЁеҜҶеәҰзҡ„дёҚеқҮеҢҖд»ҘеҸҠеӨ–йғЁзҡ„жҪ®жұҗеҠӣдҪҝеҫ—ең°зҗғзҡ„еҪўзҠ¶еҒҸзҰ»зҗғеҪўгҖӮеҗҢж—¶еұҖйғЁзҡ„ең°еҠҝеўһеӨ§дәҶиҝҷз§ҚдёҚеқҮеҢҖжҖ§пјҢдҪҝеҫ—ең°зҗғзҡ„иЎЁйқўзҠ¶еҶөжһҒеәҰеӨҚжқӮгҖӮдёәдәҶдҫҝдәҺеӨ„зҗҶпјҢеҜ№ең°зҗғиЎЁйқўзҡ„жҸҸиҝ°еҝ…йЎ»жҜ”е®һйҷ…жӣҙеҠ з®ҖеҚ•гҖӮеӣ жӯӨжҲ‘们е»әз«ӢдёҖдёӘиғҪеӨҹж»Ўи¶ійңҖиҰҒзҡ„ең°зҗғиЎЁйқўзҡ„жңҖз®ҖжЁЎеһӢгҖӮ
7 Q1 r% P8 o8 Y1 r O" I0 k
жүҖжңүиҝҷдәӣеёёз”Ёзҡ„жЁЎеһӢйғҪдјҡж¶үеҸҠеҲ°вҖңеҚҠеҫ„вҖқзҡ„жҰӮеҝөгҖӮдёҘж јең°иҜҙпјҢз«ӢдҪ“еӣҫеҪўдёӯеҸӘжңүзҗғдҪ“жүҚжңүеҚҠеҫ„зҡ„жҰӮеҝөпјҢдҪҶеңЁеҫҲеӨҡйўҶеҹҹпјҢеҢ…жӢ¬еӨ„зҗҶең°зҗғзҡ„жЁЎеһӢпјҢйғҪдјҡжү©еұ•вҖңеҚҠеҫ„вҖқзҡ„з”Ёжі•гҖӮд»ҘдёӢжҳҜжҢүз…§зІҫзЎ®еәҰйҷҚеәҸзҡ„ең°зҗғжЁЎеһӢпјҡ
* x0 ~1 Q* }5 u) N& K
ең°зҗғзҡ„зңҹе®һиЎЁйқў;
0 ~, v: W9 i ]
жҢүз…§зңҹе®һиЎЁйқўжҜҸзӮ№зҡ„е№іеқҮжө·е№ійқўе®ҡд№үзҡ„еӨ§ең°ж°ҙеҮҶйқў;
' V( V2 E! {) v- n8 v# a
еҜ№дәҺеӨ§ең°ж°ҙеҮҶйқўе’ҢжӨӯзҗғдҪ“жқҘиҜҙпјҢжЁЎеһӢдёҠд»»дҪ•дёҖзӮ№еҲ°жҢҮе®ҡдёӯеҝғзҡ„зЎ®е®ҡи·қзҰ»иў«з§°дёәвҖңең°зҗғзҡ„дёҖжқЎеҚҠеҫ„вҖқжҲ–вҖңеңЁжҹҗзӮ№ең°зҗғзҡ„еҚҠеҫ„вҖқгҖӮеҗҢж—¶д№ҹеёёз”ЁзҗғдҪ“жЁЎеһӢзҡ„вҖңе№іеқҮеҚҠеҫ„вҖқжқҘдҪңдёәвҖңең°зҗғеҚҠеҫ„вҖқгҖӮеҸҰдёҖж–№йқўпјҢеҜ№еә”ең°зҗғзңҹе®һиЎЁйқўзҡ„вҖңеҚҠеҫ„вҖқжҳҜжІЎжңүе®һйҷ…з”ЁеӨ„зҡ„гҖӮзӣёеҸҚпјҢзӣёеҜ№дәҺжө·е№ійқўзҡ„жө·жӢ”жүҚжҳҜжңүе®һйҷ…з”ЁйҖ”зҡ„гҖӮ
3 ?6 P9 t n* b: K% U; M2 T0 v
ең°зҗғзҡ„д»»дҪ•дёҖжқЎеҚҠеҫ„й•ҝеәҰйғҪиҗҪеңЁжңҖе°Ҹзҡ„зәҰдёә6,357kmзҡ„жһҒеҚҠеҫ„д»ҘеҸҠжңҖеӨ§зҡ„зәҰдёә6,378kmзҡ„иөӨйҒ“еҚҠеҫ„д№Ӣй—ҙгҖӮеӣ жӯӨең°зҗғеҪўзҠ¶дёҺж ҮеҮҶзҗғдҪ“зҡ„еҒҸе·®еҸӘжңүзәҰдёүзҷҫеҲҶд№ӢдёҖпјҢиҝҷеңЁеӨ§еӨҡж•°жғ…еҶөдёӢеҸҜд»Ҙе……еҲҶең°жҠҠең°зҗғзңӢеҒҡзҗғдҪ“并дҪҝз”ЁжңҜиҜӯвҖңең°зҗғеҚҠеҫ„вҖқгҖӮиҝҷдёӘжҰӮеҝөд№ҹеҸҜд»ҘжҺЁе№ҝеҲ°е…¶д»–дё»иҰҒзҡ„иЎҢжҳҹдёҠеҺ»пјҢеҸӘдёҚиҝҮжүҒзҺҮжңүе·®ејӮиҖҢе·ІгҖӮ
1 R1 ~* n- Z- h% |! v) _ жһҒеҚҠеҫ„
$ D+ D/ u8 u+ q( i# A+ [ д»Һең°еҝғеҲ°еҢ—жһҒжҲ–еҚ—жһҒзҡ„и·қзҰ»пјҢеӨ§зәҰ3950иӢұйҮҢ(6356.9088еҚғзұі)(дёӨжһҒзҡ„е·®жһҒе°ҸпјҢеҸҜд»ҘеҝҪз•Ҙ)гҖӮ
& X3 _* O; V" e
иөӨйҒ“еҚҠеҫ„
1 n! w! m8 g0 A2 L0 Q' ~. { жҳҜд»Һең°еҝғеҲ°иөӨйҒ“зҡ„и·қзҰ»пјҢеӨ§зәҰ3963иӢұйҮҢ(6377.830еҚғзұі)гҖӮ
4 J) Z" u7 o6 E& F9 o е№іеқҮеҚҠеҫ„
$ j5 W8 @/ k2 t' T2 D
еӨ§зәҰ3959иӢұйҮҢ(6371.393еҚғзұі) гҖӮиҝҷдёӘж•°еӯ—жҳҜең°еҝғеҲ°ең°зҗғиЎЁйқўжүҖжңүеҗ„зӮ№и·қзҰ»зҡ„е№іеқҮеҖјгҖӮ
6 l7 I3 C& ?9 i; E( S еҸҜд»Ҙиҝҷж ·жұӮпјҡе№іеқҮеҚҠеҫ„=(иөӨйҒ“еҚҠеҫ„Г—2+жһҒеҚҠеҫ„)/3
" P/ j5 N. d9 a* ~ ең°зҗғеҚҠеҫ„жңүж—¶иў«дҪҝз”ЁдҪңдёәи·қзҰ»еҚ•дҪҚ, зү№еҲ«жҳҜеңЁеӨ©ж–ҮеӯҰе’Ңең°иҙЁеӯҰдёӯеёёз”ЁгҖӮе®ғйҖҡеёёз”ЁREиЎЁзӨәгҖӮ
5 @ x- a9 r& c" C7 ` ең°зҗғеӨ§жҰӮеҚҠеҫ„6370.856еҚғзұігҖӮ
. i7 r3 u# x9 u {8 K3 { жҲ‘们зҹҘйҒ“пјҢең°зҗғзҡ„еҪўзҠ¶иҝ‘дјјдёҖдёӘзҗғеҪўпјҢйӮЈд№ҲжҖҺж ·жөӢеҮәе®ғзҡ„еҚҠеҫ„е‘ў?жҚ®иҜҙе…¬е…ғеүҚдёүдё–зәӘж—¶еёҢи…ҠеӨ©ж–ҮеӯҰ家еҺ„жӢүеӨҡеЎһеҶ…ж–Ҝ(EratosthenesпјҢе…¬е…ғеүҚ276вҖ”194)йҰ–ж¬ЎжөӢеҮәдәҶең°зҗғзҡ„еҚҠеҫ„гҖӮ
5 K0 ]5 k# N& G2 J
д»–еҸ‘зҺ°еӨҸиҮіиҝҷдёҖеӨ©пјҢеҪ“еӨӘйҳізӣҙе°„еҲ°иөӣдјҠеҹҺ(д»ҠеҹғеҸҠйҳҝж–Ҝж—әеҹҺ)зҡ„ж°ҙдә•Sж—¶пјҢеңЁдәҡеҺҶеұұеӨ§еҹҺзҡ„дёҖзӮ№Aзҡ„еӨ©йЎ¶дёҺеӨӘйҳізҡ„еӨ№и§’дёә7.2В°(еӨ©йЎ¶е°ұжҳҜй“…еһӮзәҝеҗ‘дёҠж— йҷҗ延й•ҝдёҺеӨ©з©әвҖңеӨ©зҗғвҖқзӣёдәӨзҡ„дёҖзӮ№)гҖӮд»–и®ӨдёәиҝҷдёӨең°еңЁеҗҢдёҖжқЎеӯҗеҚҲзәҝдёҠпјҢд»ҺиҖҢиҝҷдёӨең°й—ҙзҡ„еј§жүҖеҜ№зҡ„еңҶеҝғи§’SOAе°ұжҳҜ7.2В°(еҰӮеӣҫ1)гҖӮеҸҲзҹҘе•Ҷйҳҹж—…иЎҢж—¶жөӢеҫ—AгҖҒSй—ҙзҡ„и·қзҰ»зәҰдёә5000еҸӨеёҢи…ҠйҮҢпјҢд»–жҢүз…§еј§й•ҝдёҺеңҶеҝғи§’зҡ„е…ізі»пјҢз®—еҮәдәҶең°зҗғзҡ„еҚҠеҫ„зәҰдёә4000еҸӨеёҢи…ҠйҮҢгҖӮдёҖиҲ¬и®Өдёә1еҸӨеёҢи…ҠйҮҢзәҰдёә158.5зұіпјҢйӮЈд№Ҳд»–жөӢеҫ—ең°зҗғзҡ„еҚҠеҫ„зәҰдёә6340е…¬йҮҢгҖӮ
; c1 b4 c0 ^( m' c& [
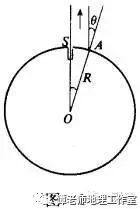
9 p; j3 X8 ?" o е…¶еҺҹзҗҶдёәпјҡ
7 _( y# R( C2 \2 p; T q8 D" k и®ҫеңҶе‘Ёй•ҝдёәCпјҢеҚҠеҫ„дёәRпјҢдёӨең°й—ҙзҡ„зҡ„еј§й•ҝдёәLпјҢеҜ№еә”зҡ„еңҶеҝғи§’дёәnВ°гҖӮ
2 t" ?/ d0 O. C& i8 `/ e
еӣ дёә360В°зҡ„еңҶеҝғи§’жүҖеҜ№зҡ„еј§й•ҝе°ұжҳҜеңҶе‘Ёй•ҝC=2ПҖRпјҢжүҖд»Ҙ1В°зҡ„еңҶеҝғи§’жүҖеҜ№еј§й•ҝжҳҜ
4 N6 X* }* }' A- o 
/ X5 U) Y& t9 B6 L! V
пјҢеҚі
) i! `5 M+ K# B u6 c 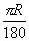
9 x$ o& F T3 R& O" U" Q5 `# `8 V
гҖӮдәҺжҳҜеҚҠеҫ„дёәзҡ„Rзҡ„еңҶдёӯпјҢnВ°зҡ„еңҶеҝғи§’жүҖеҜ№зҡ„еј§й•ҝLдёәпјҡ
" R. O1 X# @1 q
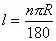
, q+ k* C% ^; Z- U% w& f+ t2 @- w: Y& {
гҖӮ
4 g+ L$ h6 _/ E/ V" y. }6 r) s
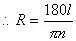
8 r7 y- b e$ Q6 F5 h
гҖӮ
f z9 U7 n! E( l |0 j7 C еҪ“L=5000еҸӨеёҢи…ҠйҮҢпјҢn=7.2ж—¶пјҢ
3 G. ?% l; l7 m$ H7 E% S+ |& f$ @) e
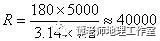
( D+ J* [6 L: |
еҸӨеёҢи…ҠйҮҢ) еҢ–дёәе…¬йҮҢж•°дёәпјҡ
3 Z( E. S/ C7 I1 u' a- }# C

. P4 O& U# d: J/ j7 x; r. w! N( {
(е…¬йҮҢ)гҖӮ
1 _: F! }/ k. |
еҺ„жӢүеӨҡеЎһеҶ…ж–Ҝиҝҷз§ҚжөӢең°зҗғзҡ„ж–№жі•еёёз§°дёәеј§еәҰжөӢйҮҸжі•гҖӮз”Ёиҝҷз§Қж–№жі•жөӢйҮҸж—¶пјҢеҸӘиҰҒжөӢеҮәдёӨең°й—ҙзҡ„еј§й•ҝе’ҢеңҶеҝғи§’пјҢе°ұеҸҜжұӮеҮәең°зҗғзҡ„еҚҠеҫ„дәҶгҖӮ
' R' v8 p" m6 l6 Z) ^! \# t9 g( J4 w иҝ‘д»ЈжөӢйҮҸең°зҗғзҡ„еҚҠеҫ„пјҢиҝҳз”Ёеј§еәҰжөӢйҮҸзҡ„ж–№жі•пјҢеҸӘжҳҜеңЁжұӮзӣёи·қеҫҲиҝңзҡ„дёӨең°й—ҙзҡ„и·қзҰ»ж—¶пјҢйҮҮз”ЁдәҶеёғи®ҫдёүи§’зҪ‘зҡ„ж–№жі•гҖӮжҜ”еҰӮжұӮMгҖҒNдёӨең°зҡ„и·қзҰ»ж—¶пјҢеҸҜд»ҘеғҸеӣҫ2йӮЈж ·еёғи®ҫдёүи§’зӮ№пјҢз”Ёз»Ҹзә¬д»ӘжөӢйҮҸеҮәв–іAMBпјҢв–іABCпјҢв–іBCDпјҢв–іCDEпјҢв–іEDNзҡ„еҗ„дёӘеҶ…и§’зҡ„еәҰж•°пјҢеҶҚйҮҸеҮәMзӮ№йҷ„иҝ‘зҡ„йӮЈжқЎеҹәзәҝMAзҡ„й•ҝпјҢжңҖеҗҺеҚіеҸҜз®—еҮәMNзҡ„й•ҝеәҰдәҶгҖӮ
* s4 Y1 a' E8 d, r! P 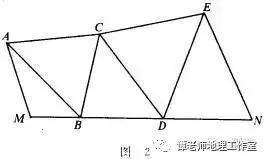
4 a) q7 F2 f+ m, b; m0 K* `
йҖҡиҝҮиҝҷдәӣдёүи§’еҪўпјҢжҖҺж ·з®—еҮәMNзҡ„й•ҝеәҰе‘ў?иҝҷйҮҢиҰҒз”ЁеҲ°дёүи§’еҪўзҡ„дёҖдёӘеҫҲйҮҚиҰҒзҡ„е®ҡзҗҶвҖ”вҖ”жӯЈејҰе®ҡзҗҶгҖӮ
- M) m' E! a" ?! S7 C6 D
еҚіпјҡеңЁдёҖдёӘдёүи§’еҪўдёӯпјҢеҗ„иҫ№е’Ңе®ғжүҖеҜ№и§’зҡ„жӯЈејҰзҡ„жҜ”зӣёзӯүгҖӮе°ұжҳҜиҜҙпјҢеңЁв–іABCдёӯпјҢжңү
- j! q+ \, {2 k$ ?; W; V
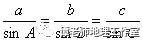
$ ~% u {/ k1 e1 y& I$ r, h8 p
гҖӮ
2 Q& X% ~9 W3 s! |2 \+ ?( `, I еңЁеӣҫ2дёӯпјҢз”ұдәҺеҗ„дёүи§’еҪўзҡ„еҶ…и§’е·ІжөӢеҮәпјҢAMзҡ„й•ҝд№ҹйҮҸеҮәпјҢз”ұжӯЈејҰе®ҡзҗҶеҚіеҸҜеҲҶеҲ«з®—еҮәпјҡ
- h+ L# u. O2 M+ w3 `
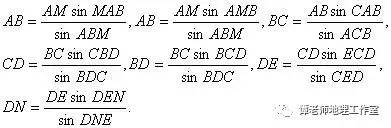
6 f a2 b0 y: ?: O; \! i- ?. z# N3 g вҲҙMN=MB+BD+DNгҖӮ
1 A `5 j" U; m
еҰӮжһңMгҖҒNдёӨең°еңЁеҗҢдёҖжқЎеӯҗеҚҲзәҝдёҠпјҢз”ЁеӨ©ж–Үж–№жі•жөӢеҮәеҗ„ең°зҡ„зә¬еәҰеҗҺпјҢеҚіеҸҜз®—еҮәеӯҗеҚҲзәҝ1В°зҡ„й•ҝеәҰгҖӮжі•еӣҪзҡ„зҡ®еҚЎе°”(Pi-card.J.1620вҖ”1682)дәҺ1669вҖ”1671е№ҙзҺҮйўҶд»–зҡ„жөӢйҮҸйҳҹйҰ–ж¬ЎжөӢеҮәдәҶе·ҙй»Һе’Ңдәҡзң д№Ӣй—ҙзҡ„еӯҗеҚҲзәҝзҡ„й•ҝпјҢжұӮеҫ—еӯҗеҚҲзәҝ1В°зҡ„й•ҝзәҰдёә111.28е…¬йҮҢпјҢиҝҷж ·д»–жҺЁз®—еҮәең°зҗғзҡ„еҚҠеҫ„зәҰдёә6376е…¬йҮҢгҖӮ
* d& X5 Y+ C3 D) X2 l6 A4 E 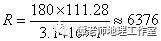
1 A6 b) j+ i! C. [ (е…¬йҮҢ)гҖӮ
3 [* s N2 `& O' h( _, Z8 @& p еҸҰеӨ–пјҢеёғи®ҫдёүи§’зҪ‘жңүеӨҡз§Қж–№жі•пјҢиҰҒж №жҚ®е®һйҷ…жғ…еҶөпјҢеёғи®ҫзҡ„зҪ‘зӮ№и¶Ҡе°‘и¶ҠеҘҪгҖӮ
# ~: x; h1 m6 j# U1 T- L5 g+ C
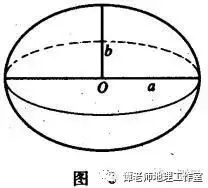
йҡҸзқҖ科еӯҰзҡ„еҸ‘еұ•пјҢдәә们еҜ№ең°зҗғзҡ„и®ӨиҜҶд№ҹи¶ҠжқҘи¶Ҡж·ұе…ҘпјҢ并еҸ‘зҺ°ең°зҗғдёҚе®Ңе…ЁжҳҜзҗғеҪўзҡ„пјҢиҖҢжҳҜдёҖдёӘжӨӯзҗғдҪ“(еҰӮеӣҫ3)гҖӮ科еӯҰ家家们иҝҳжүҫеҲ°дәҶжұӮеҫ—ең°зҗғзҡ„й•ҝеҚҠеҫ„aе’ҢзҹӯеҚҠеҫ„bзҡ„ж–№жі•пјҢз”ұдәҺжҜ”иҫғеӨҚжқӮпјҢжҲ‘们иҝҷйҮҢе°ұдёҚд»Ӣз»ҚдәҶпјҢжңүе…ҙи¶Јзҡ„еҗҢеӯҰеҸҜйҳ…иҜ»жңүе…ід№ҰзұҚгҖӮ
* h$ f j4 B: u3 w( @9 |
5 M2 O$ Q4 \# Q2 l. K
дҪ зӣёдҝЎеҗ—пјҢд»…д»…еҲ©з”ЁдёҖеј ж—ҘиҗҪзҡ„з…§зүҮпјҢдҪ е°ұиғҪеҫ—еҮәең°зҗғзҡ„еҚҠеҫ„еӨ§е°Ҹ! Princeton еӨ§еӯҰзҡ„ Robert Vanderbei еңЁжңҖиҝ‘зҡ„дёҖзҜҮи®әж–ҮдёӯеҜ№дёҖеј ж‘„дәҺеҜҶжӯҮж №ж№–зҡ„ж—ҘиҗҪз…§зүҮиҝӣиЎҢдәҶеҲҶжһҗпјҢдёҚдҪҶиҜҒе®һдәҶең°зҗғжҳҜеңҶзҡ„пјҢиҝҳдҫқжҚ®з…§зүҮдёҠзҡ„еҶ…е®№еҜ№ең°зҗғеҚҠеҫ„иҝӣиЎҢдәҶдј°з®—гҖӮ
& ?9 s3 r, }, X; |

. \: i6 ~& F2 a5 X6 ^& b дәӢжғ…зҡ„иө·еӣ е°ұжҳҜдёҠйқўиҝҷеј еҫҲе№іеёёзҡ„ж—ҘиҗҪз…§зүҮпјҢд»ҘеҸҠиҝҷж ·дёҖдёӘеӨ§е®¶е№іж—¶е№¶жІЎжңүеӨӘеңЁж„Ҹзҡ„й—®йўҳпјҡеӨӘйҳійңІеҮәж°ҙйқўзҡ„йғЁеҲҶеә”иҜҘжҳҜдёҖдёӘж ҮеҮҶзҡ„еј“еҪўпјҢдҪҶдёәд»Җд№ҲеңЁж—ҘеҮәж—ҘиҗҪж—¶пјҢжҲ‘们жүҖзңӢеҲ°зҡ„еӨӘйҳіжҳҜдёҖдёӘж©„жҰ„зҗғдёҖж ·зҡ„еҪўзҠ¶?еӨ§е®¶жҲ–и®ёдјҡеҫҲеҝ«жғіеҲ°пјҢеҸ‘е…үдҪ“зҡ„дёӢеҚҠйғЁеҲҶе…¶е®һжҳҜж—Ҙе…үеҸҚе°„еңЁж°ҙйқўдёҠйҖ жҲҗзҡ„гҖӮйҡҸд№Ӣдә§з”ҹзҡ„жҳҜеҸҰдёҖдёӘй—®йўҳпјҡдёәд»Җд№Ҳе®ғзҡ„дёӢеҚҠйғЁеҲҶиҰҒжҜ”дёҠеҚҠйғЁеҲҶе°ҸдёҖдәӣе‘ў?
U0 S2 G% r* \9 [$ o) H9 c 
2 h9 |7 K9 r7 ?: m: [; e u
иҝҷжҳҜеӣ дёәвҖ”вҖ”жғіеҲ°иҝҷдёӘй—®йўҳзҡ„зӯ”жЎҲ并дёҚе®№жҳ“вҖ”вҖ”ең°зҗғжҳҜеңҶзҡ„гҖӮдёҠеӣҫе°ұжҳҜдәәз«ҷеңЁең°зҗғдёҠзңӢж—ҘеҮәзҡ„дёҖдёӘжҜ”дҫӢеӨёеј зүҲзӨәж„ҸеӣҫпјҢе…¶дёӯ O дёәең°зҗғзҡ„дёӯеҝғпјҢ A дёәдәәзңјзҡ„дҪҚзҪ®пјҢ AB дёәи§Ҷе№ізәҝпјҢ B зӮ№дёәж°ҙеӨ©дәӨз•ҢеӨ„гҖӮз”ұдәҺеӨӘйҳіи·қзҰ»жҲ‘们зӣёеҪ“йҒҘиҝңпјҢеӣ жӯӨжҲ‘们жҠҠеӨӘйҳіе…үзңӢдҪңжҳҜдёҖжқҹзҗҶжғізҡ„е№іиЎҢе…үзәҝгҖӮжҲ‘们жҠҠзӣҙжҺҘе°„е…Ҙдәәзңјзҡ„еӨӘйҳіе…үдёҺ AB зҡ„еӨ№и§’и®°дёә Оұ пјҢжҠҠз»ҸиҝҮж°ҙйқўдёҠзҡ„дёҖзӮ№ C еҸҚе°„иҝӣе…Ҙдәәзңјзҡ„е…үзәҝдёҺ AB зҡ„еӨ№и§’и®°дёә ОІ гҖӮд»ҺеӣҫдёҠеҸҜи§ҒпјҢи§Ҷи§’ ОІ жҜ” Оұ е°ҸпјҢд№ҹе°ұжҳҜиҜҙеӨӘйҳіеңЁж°ҙйқўдёҠзҡ„й•ңеғҸжҜ”жң¬иә«иҰҒе°ҸдёҖдәӣгҖӮ
! V$ b) g! J7 k3 j1 u

5 Q6 Q6 `* i2 p1 ^
ОІ 究з«ҹжҜ” Оұ е°ҸеӨҡе°‘е‘ў?еҜ№з…§зүҮиҝӣиЎҢзІҫзЎ®ең°жөӢйҮҸпјҢеҸҜзҹҘеӨӘйҳізҡ„зӣҙеҫ„зӣёеҪ“дәҺз…§зүҮдёӯзҡ„ 317 дёӘеғҸзҙ пјҢиҖҢйңІеҮәж°ҙйқўзҡ„йғЁеҲҶй«ҳ 69 еғҸзҙ пјҢж°ҙдёӯзҡ„еҖ’еҪұеҲҷеҸӘжңү 29 еғҸзҙ гҖӮдј—жүҖе‘ЁзҹҘеӨӘйҳізҡ„и§Ҷзӣҙеҫ„(зңӢеӨӘйҳізҡ„и§Ҷи§’)дёә 0.5 еәҰпјҢеӣ жӯӨжҲ‘们е°ұеҫ—еҲ° Оұ = 0.5 * 69 / 317 вүҲ 0.1088 еәҰпјҢ ОІ = 0.5 * 29 / 317 вүҲ 0.0457 еәҰгҖӮ
2 p# b, W! g6 A, i
еҰӮжһңеҶҚе·ІзҹҘдәәзңј(жҲ–иҖ…иҜҙзӣёжңә)зҰ»ж°ҙйқўзҡ„еһӮзӣҙи·қзҰ» h дёә 2 зұіпјҢйӮЈд№Ҳж №жҚ®иҝҷдәӣж•°жҚ®жҲ‘们е°ұи¶ід»Ҙдј°з®—еҮәең°зҗғзҡ„еҚҠеҫ„дәҶгҖӮдёҚеҰЁжҠҠ вҲ AOB и®°дёә ПҶ пјҢжҠҠ вҲ AOC и®°дёә Оё пјҢжҠҠдәәзңјеҲ°ж°ҙеӨ©зӣёжҺҘеӨ„зҡ„и·қзҰ» AB и®°дёә D пјҢжҠҠдәәзңјеҲ°еҸҚе°„зӮ№зҡ„и·қзҰ» AC и®°дёә d пјҢе…Ҙе°„и§’е’ҢеҸҚе°„и§’и®°дёә Оі пјҢжңҖеҗҺз”Ё r жқҘиЎЁзӨәең°зҗғеҚҠеҫ„пјҢйӮЈд№ҲжӯӨж—¶жҲ‘们дёҖе…ұжңү 6 дёӘжңӘзҹҘйҮҸгҖӮдёәдәҶжұӮи§ЈеҮәиҝҷ 6 дёӘжңӘзҹҘж•°пјҢжҲ‘们йңҖиҰҒеҜ»жүҫ 6 дёӘдёҚеҗҢзҡ„ж–№зЁӢгҖӮиҝҷ 6 дёӘж–№зЁӢеҸҜд»Ҙз”ұд»ҘдёӢ 6 з»„зӯүйҮҸе…ізі»еҫ—еҲ°пјҡ
3 Y. A/ b# c9 D. G1 c; F q. y Q 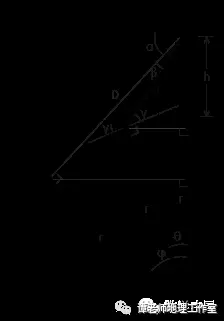
# p$ b( w8 @0 \4 r6 A* } 1. еӣӣиҫ№еҪў OBAC зҡ„еҶ…и§’е’Ңдёә 360В° пјҢеҚі (ПҶ - Оё) + 90В° + ОІ + (180В° - Оі + 90В°) = 360В° пјҢ еҢ–з®Җеҫ— ж–№зЁӢ(1) ПҶ + ОІ = Оё + Оі
$ O7 l& w% u1 N/ b6 v- M; u 2. дёӨжқЎе№іиЎҢзәҝзҡ„еҗҢж—ҒеҶ…и§’зӣёеҠ дёә 180В° пјҢеҚі (Оұ + ОІ) + (180В° - 2Оі) = 180В° пјҢеҚі ж–№зЁӢ(2) Оұ + ОІ = 2Оі
( ^* x+ T; B- p. W3 L
3. з”ұдәҺ AO = h + r пјҢеҗҢж—¶еҸҲжңү AO = AD + DO = DВ·sinПҶ + rВ·cosПҶ пјҢеӣ жӯӨжңү ж–№зЁӢ(3) h + r = DВ·sinПҶ + rВ·cosПҶ
$ O& E* o: _% F" J9 K) K. ? 4. BD ж—ўеҸҜд»ҘзӯүдәҺ DВ·cosПҶ пјҢеҸҲеҸҜд»ҘзӯүдәҺ rВ·sinПҶ пјҢдәҺжҳҜжңү ж–№зЁӢ(4) DВ·cosПҶ = rВ·sinПҶ
5 I0 Q/ ]9 g) T; a: k( ?: R 5. з”ұдәҺ AO = h + r пјҢеҗҢж—¶еҸҲжңү AO = AE + EO = dВ·sin(Оі+Оё) + rВ·cosОё пјҢеӣ жӯӨжңү ж–№зЁӢ(5) h + r = dВ·sin(Оі+Оё) + rВ·cosОё
7 S0 d* p( D+ O8 t
6. CE ж—ўеҸҜд»ҘзӯүдәҺ dВ·cos(Оі+Оё) пјҢеҸҲеҸҜд»ҘзӯүдәҺ rВ·sinОё пјҢдәҺжҳҜжңү ж–№зЁӢ(6) dВ·cos(Оі+Оё) = rВ·sinОё
8 O9 A! O) Y* a дёҖзі»еҲ—еӨҚжқӮзҡ„д»Јж•°иҝҗз®—(зңҒз•Ҙж•°зҷҫеӯ—)жңҖз»Ҳе‘ҠиҜүжҲ‘们пјҡ
+ A8 G/ r3 f/ H
r = h / (вҲҡ1 - 2В·cosОІВ·cosОі + cos2Оі / sinОІ - 1)
' ^. A' O+ k; O9 H4 a
е…¶дёӯ Оі = (Оұ + ОІ)/2 гҖӮд»Је…Ҙе·ІзҹҘзҡ„ Оұ гҖҒ ОІ е’Ң h еҸҜд»Ҙеҫ—еҲ°пјҢең°зҗғеҚҠеҫ„ r еӨ§зәҰдёә 7.29312 * 106 зұіпјҢд№ҹеҚі 7293 еҚғзұігҖӮ
8 l# e* K% G5 `, ]5 h( @
иҝҷдёӘдј°з®—зҡ„иҜҜе·®жңүеӨҡеӨ§е‘ў?дәӢе®һдёҠпјҢең°зҗғзҡ„еҚҠеҫ„еӨ§зәҰдёә 6300 еӨҡеҚғзұіпјҢеҸҜи§ҒиҜҜе·®дёҚжҳҜдёҖиҲ¬зҡ„еӨ§гҖӮдёҚиҝҮпјҢиҖғиҷ‘еҲ°жҲ‘们估算зҡ„дҫқжҚ®д»…д»…жҳҜдёҖеј з…§зүҮпјҢиғҪжҠҠж•°йҮҸзә§дј°еҜ№е°ұе·Із»ҸзӣёеҪ“зүӣ B дәҶгҖӮйҷӨдәҶжөӢйҮҸзҡ„зІҫеәҰд№ӢеӨ–пјҢиҝҳжңүеҫҲеӨҡжҪңеңЁзҡ„еӣ зҙ дјҡеҜјиҮҙиҜҜе·®гҖӮзӣ®еүҚзңӢжқҘпјҢиҜҜе·®зҡ„жңҖдё»иҰҒжқҘжәҗдјјд№ҺжҳҜдёҚе®Ңе…Ёе№ійқҷзҡ„ж°ҙйқўвҖ”вҖ”дёҖзӮ№е°Ҹе°Ҹзҡ„жіўжөӘе°ұдјҡз»ҷ Оұ гҖҒ ОІ зҡ„еҖјеёҰжқҘе·ЁеӨ§зҡ„еҪұе“ҚгҖӮ
4 u, E* Y* l1 K

* Z/ U- f, Z9 u1 t* v5 G9 P$ W/ A
е…¬е…ғеүҚ3 дё–зәӘпјҢеҸӨеёҢи…ҠеӨ©ж–ҮеӯҰ家еҹғжӢүжүҳиүІе°јйҰ–ж¬ЎжөӢйҮҸеҮәдәҶең°зҗғзҡ„еҚҠеҫ„гҖӮд»–еҸ‘зҺ°еӨҸиҮіиҝҷдёҖеӨ©пјҢеҪ“еӨӘйҳізӣҙе°„еҲ°иөӣеӣ еҹҹ(д»ҠеҹғеҸҠйҳҝж–Ҝж—әеҹҺйҷ„иҝ‘)зҡ„ж°ҙдә•ж—¶пјҢеңЁдәҡеҺҶеұұеӨ§еҹҺзҡ„дёҖзӮ№зҡ„еӨ©йЎ¶дёҺеӨӘйҳізҡ„еӨ№и§’дёә7.2В°гҖӮд»–и®ӨдёәиҝҷдёӨең°еңЁеҗҢдёҖжқЎеӯҗеҚҲзәҝдёҠпјҢд»ҺиҖҢиҝҷдёӨең°й—ҙзҡ„еј§жүҖеҜ№зҡ„еңҶеҝғи§’е°ұжҳҜ7.2В°гҖӮеҸҲзҹҘе•Ҷйҳҹж—…иЎҢж—¶жөӢеҫ—дёӨең°й—ҙзҡ„и·қзҰ»зәҰдёә5000 еҸӨеёҢи…ҠйҮҢпјҢд»–жҢүз…§еј§й•ҝдёҺеңҶеҝғи§’зҡ„е…ізі»пјҢз®—еҮәдәҶең°зҗғзҡ„еҚҠеҫ„зәҰдёә40 000 еҸӨеёҢи…ҠйҮҢгҖӮ
+ h& c+ ]0 P$ f; Z! }
д»–жҳҜжҖҺд№Ҳз®—зҡ„е‘ў?жҲ‘们дёҚеҰЁи·ҹеҸӨеёҢи…ҠдәәдёҖиө·жқҘеҒҡйҒ“ж•°еӯҰйўҳпјҡеҒҮи®ҫеңҶе‘Ёй•ҝдёәCпјҢеҚҠеҫ„дёәrпјҢдёӨең°й—ҙзҡ„еј§й•ҝдёәlпјҢеҜ№еә”зҡ„еңҶеҝғи§’дёәОёгҖӮеӣ дёә360В°зҡ„еңҶеҝғи§’жүҖеҜ№зҡ„еј§й•ҝжҳҜеңҶе‘Ёй•ҝC=2ПҖrпјҢжүҖд»Ҙ1В°зҡ„еңҶеҝғи§’жүҖеҜ№еә”зҡ„еј§й•ҝй•ҝеәҰжҳҜ2ПҖr / 360пјҢеҚіПҖr / 180гҖӮдәҺжҳҜпјҢеҚҠеҫ„дёәr зҡ„еңҶдёӯпјҢеңҶеҝғи§’ОёжүҖеҜ№зҡ„еј§й•ҝl дёәпјҡl=ОёПҖr / 180гҖӮжүҖд»ҘпјҢr=180 l / (ОёПҖ)гҖӮ
, f2 t* c; a' l6 x* I( U. s' U- x еҪ“дёӨең°и·қзҰ»l дёә5000 еҸӨеёҢи…ҠйҮҢпјҢОёзӯүдәҺ7.2 В°ж—¶пјҢ е°ұз®—еҮәең°зҗғеҚҠеҫ„r жҳҜ180Г—5000/(7.2Г—3.141 59 ) вүҲ 40 000 еҸӨеёҢи…ҠйҮҢгҖӮжӣҫжңүдәәиҖғиҜҒпјҢ1 еҸӨеёҢи…ҠйҮҢзәҰдёәзҺ°еңЁзҡ„158 зұіпјҢжҢүиҝҷдёӘе…ізі»жҚўз®—пјҢ40 000 еҸӨеёҢи…ҠйҮҢеҲҷзӣёеҪ“дәҺзҺ°еңЁзҡ„6300 еҚғзұігҖӮ
' z/ ~4 H$ ^: i- F) A2 d, T4 l, | иҝҷз§ҚжөӢең°зҗғзҡ„ж–№жі•еёёз§°дёәеј§еәҰжөӢйҮҸжі•гҖӮз”Ёиҝҷз§Қж–№жі•жөӢйҮҸж—¶пјҢеҸӘиҰҒжөӢеҮәдёӨең°й—ҙзҡ„еј§й•ҝе’ҢеңҶеҝғи§’пјҢе°ұеҸҜжұӮеҮәең°зҗғзҡ„еҚҠеҫ„дәҶгҖӮ
. `$ B' s; `( Z зҺ°д»ЈжөӢйҮҸең°зҗғзҡ„еҚҠеҫ„пјҢиҝҳжҳҜз”Ёеј§еәҰжөӢйҮҸзҡ„ж–№жі•пјҢжі•еӣҪзҡ„зҡ®еҚЎе°”дәҺ1669вҖ”1671 е№ҙзҺҮйўҶжөӢйҮҸйҳҹйҰ–ж¬ЎжөӢеҮәдәҶе·ҙй»Һйҷ„иҝ‘еӯҗеҚҲзәҝ1В°зҡ„й•ҝзәҰдёә111.28еҚғзұіпјҢд»ҺиҖҢжҺЁз®—еҮәең°зҗғзҡ„еҚҠеҫ„зәҰдёә6376 еҚғзұігҖӮ
5 ` B# H0 s+ V5 D/ S3 W) O9 r2 v


