( n2 j7 m' W5 n4 b, e, l& u
6.2 绘制分形; R! _* l1 |1 \; F! i+ a
分形势复杂的几何图案或形状,但却由简单的数学公式所生成。与圆形和矩形等几何图形相比,分形看上去并不规则,也没有明显的模式或描述。但如果仔细观察,你将发现模式的存在,即整个图形有无数个自身的副本构成。由于分形设计平面上的点的相同几何变换的重复引用,因此非常适合使用计算机程序来构建。这一章中,我们将学习如何绘制Barnsley蕨类植物、Sierpinski三角和Manderlbrot集合(后两个出现在编程挑战中),这些都是分形研究领域的常见例子。分形在自然界中比比皆是,常见的例子包括海岸线、树木和雪花。
, |9 m& K. H/ E* r 6.2.1 平面上点的变化
5 U+ A2 l+ n0 `6 L+ x) ^! L 创建分形的基本思想是点的变换。给定x-y平面上的一个点P(x,y),变幻的一个例子是P(x,y)->Q(x+1, y+1),这意味着应用变换后,创建好了一个新点Q,它位于P向上和向右各一个单位处。如果以Q点作为起始点,将得到另一个点R,它位于点Q向上和向右各一个单位处。假设起始点P位于(1,1),下图展示了这些点的位置。 ; i' h7 P$ G) \% D4 X) Y' ~$ d6 l
 1 |- M, ^5 c# e7 V8 T5 W: b$ Z8 R
1 |- M, ^5 c# e7 V8 T5 W: b$ Z8 R P、Q、R三个点的位置图
1 n% T7 s, @ ^) |/ M4 t5 G, x1 V 因此,变换是一种描述点在x-y平面上移动的规则,从起始位置开始,每一次迭代使得点移动到新的位置。我们可以把变换想象成点在平面上的轨迹。现在换个思路考虑两个变换规则,每次迭代将从这两个规则中随机选择一个。两个规则如下:
9 p! M( H$ H8 P7 c7 n/ u 规则1:P1(x,y) -> P2(x+1, y-1)
5 R6 r3 i( }$ `3 g { 规则2:P1(x,y) -> P2(x+1, y+1)
8 D) ^0 h' X5 E. F2 x 以P(1, 1)作为起始点,如果我们执行4次迭代,将得到以下一系列的点:
5 |& Z# ^5 [& f2 n+ O# I0 X! X P1(1, 1) -> P2(2, 0) (规则1) 8 o% C- r) f, G' j
P2(2, 0) -> P3(3, 1) (规则2)
" W* H7 r ]) Q2 G! x0 |) c& } P3(3, 1) -> P4(4, 2) (规则2) 5 O+ P$ M) ?7 w; }: p
P4(4, 2) -> P5(5, 1) (规则2) * U- |: M* e( t# y2 A9 d: y
...
4 R5 g6 K2 y" e! g, l 两个变换规则是随机选择的,其中每个规则被选择的概率相同。无论选择哪一个规则,点都会右移,因为在两种规则中都会增加x坐标。当点向右移动时,他们会向上或向下移动,从而形成一条Z字路径。以下程序绘制了在指定的迭代次数内进行上述转换规则之一时点的路径: . _' V, ]3 x' [* w
Example of selecting a transformation from two equally probable! |4 B) j$ y" O: n* H7 {2 Y. o6 h- ?
transformations2 M7 j3 y9 {9 u) {
6 J2 P) ?1 w ?$ e# }
import matplotlib.pyplot as plt4 p2 _0 t$ z' o% U3 y$ I# ^
import random
. B. {, Q0 @6 f/ G) T- X. c6 w! N' P7 q; [3 r) R5 Y
def transformation_1(p):
" Z; n1 j) O& [/ k/ V- K- U% f x = p[0]* `3 t- `! Q! c) ~- K/ j( k ]
y = p[1]
* }' o0 _# n5 w9 A return x + 1, y - 1
' u) K8 U' Q6 s5 I; |* a7 M+ y def transformation_2(p):
& j B, x( Z7 n6 O; @; `5 m0 \7 w x = p[0]
5 ]) c2 y! Y, c0 m. T4 z8 T y = p[1]
/ I2 y" s4 {3 f, a) n, x return x + 1, y + 1. W c# v# U. r% ^' v( L
def transform(p):* o5 I4 g- B: y
# List of transformation functions
1 M* n: [6 s5 C: Z7 j transformations = [transformation_1, transformation_2]( i' E2 y* n; Q& g7 @ y
# pick a random transformation function and call it! q* b y) `6 S' q
t = random.choice(transformations)
' U Q( i# i, o6 m x, y = t(p)- l/ B& M6 R7 C3 H
return x, y
3 c2 A% v+ y; t def build_trajectory(p, n):* Y: x' p' j5 k3 |) e }, d
x = [p[0]]
; c' o: o1 w% a. R2 b) f' s0 a5 q5 y y = [p[1]]' _: ^' {1 L: M( P8 d
for i in range(n):1 k% Y7 q) b1 K2 Y0 v7 z( e& }
p = transform(p)3 j$ B5 D$ ~/ t# i, T% s( `
x.append(p[0])0 T1 X4 K* K5 D( S$ k
y.append(p[1])
" Q& X. _$ z! K( V3 D return x, y' t4 D0 h$ n0 u3 N4 V
. g9 @ t+ _/ Z2 f4 z- E% R
if __name__ == __main__:
2 q6 H1 R# a8 N. m( ^ # Initial point
! d/ x1 k. ~; G& |0 R p = (1,1)
/ W; Y6 w0 {- Z$ H7 v9 X n = int(input(Enter the number of iterations: ))/ T0 U. p9 N: i; \
x , y = build_trajectory(p, n)- {# I4 Y- `: L4 s$ I5 k7 ]. H
# PLot
$ _5 c& n8 f. ?7 Y0 c plt.plot(x, y)
4 x# R# G1 S! G6 [ plt.xlabel(X): X5 C) V( g; \4 g( L4 {2 ^
plt.ylabel(Y)+ X9 ^6 s, O+ Y$ ^
plt.show()我们定义了两个函数transformation_1()和transformation_2(),分别对应于之前的两种变换规则,在transform()函数中,我们创建了一个包含这两个函数名字的列表,然后使用random.choice()函数从该列表中选择去哦中一个进行变换。现在假设我们选择了其中一个变换,蒋点P作为输入参数调用该变换函数,然后分别使用x,y来存储变换后的坐标并且返回它们。 4 Z$ J8 E% Y/ w/ y
从列表中随机选择一个元素 # N* N2 E7 i' d8 f) f! F3 ^) Y
我们在第一个分形程序中看到的random.choice()函数可以用来从列表中随机选择一个元素,每一个元素被选中的概率相同,下面是一个例子: import random% W- o. \) |. x" v$ U w( d
>>> l = [1,2,3]
. \% _" @2 {0 u1 q; ~ >>> random.choice(l)
/ D; @3 Z# b5 ] 1" |- o7 C7 U* A" _8 z) e
>>> random.choice(l)* d+ J' `" s' h, @! w
3
: ~( {& [, O. U. e1 g >>> random.choice(l)* z( p, g6 H1 M5 {+ r4 O3 b
37 t; ^) Q, N9 h d
>>> random.choice(l)
3 @0 p8 A1 p% U" \! T; M; f 1; C6 u, N' e5 S9 K6 z
>>> random.choice(l)4 @1 e; F& H U3 C1 E
1
; m5 |& l# ?* h8 R% a$ |$ u 这个函数也适用于元组和字符串。在后一种情形中,函数从字符串中随即返回一个字符。 . ~! b4 Q% j* B. ^& X
当运行程序,他首先会询问迭代次数n,即应用变化的次数。然后调用build_trajectory()函数,该函数的输入参数为迭代次数n和起始点坐标p,此处设置初始点坐标为(1,1)。build_trajectory()函数重复调用n次transform()函数,并使用两个列表x和y分别存储变换后的x和y坐标。最后使用这两个列表来绘制图形。
1 N1 ~# j& g) L" M 下面两张图分别显示了100次和10000次迭代的点的轨迹图,这两幅图中的Z字形运动都很明显,这种Z字形路径通常被称为一条线上的随机游走。 5 K3 P6 R9 O& P1 \( O: L! @
 7 @( T$ }1 D/ |1 u
7 @( T$ }1 D/ |1 u 迭代100次的Z字路径 + }, N& S1 @: h* A3 i
 $ A1 h5 o. e8 A( {, @/ P: [, L" S
$ A1 h5 o. e8 A( {, @/ P: [, L" S 迭代10000次的Z字路径
" {* M8 A+ W4 J- J1 t& D* c% M. Q6 k 这个例子展示了创建分形的基本思想,即从一个点开始并对其重复应用某种变换。接下来,我们将看到一个用相同想法绘制Barnsley蕨类植物的例子。
3 b! d) P- s9 M; A# G( K$ j: \ 6.2.2 绘制Barnsley蕨类植物8 @4 l- [0 j1 c7 w9 a! M. A
英国数学家Michael Barnsley描述了如何对一个点进行重复的简单变换,从而创建蕨类植物的结构(如下图)。 8 {, V; S% B, a8 A: o
 " U2 D: h8 c( l" Q, I, w! O " U2 D: h8 c( l" Q, I, w! O
蕨类植物
6 h- b% w0 x- U 他提出了以下步骤来创建类似于蕨类植物的结构,以(0,0)为初始点,按事先分配的概率随机选择下述某种变换。
% y7 X( ]2 Q2 v% G6 h+ a# K) _ (1)变换1(概率为0.85):
' m- p+ F; R/ G; s& g: e- ` 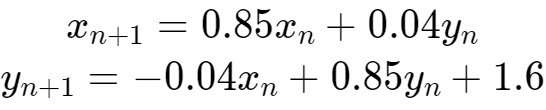
$ W( y' `3 c" z (2)变换2(概率为0.07): 1 ?) [3 N* U1 X! j' e
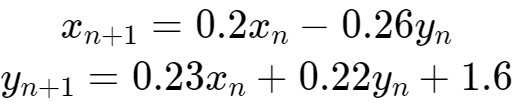
0 [# ]" B6 W% }
(3)变换3(概率为0.07): # G2 ]" u5 e+ V7 Y0 }
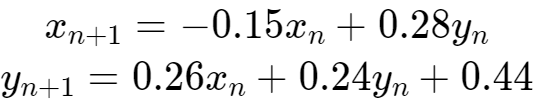
, W$ y1 R V$ C$ U4 c- h
(4)变换4(概率为0.01): & ?2 j; h! n: u. u. _: ]
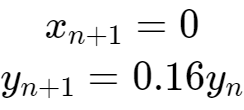
2 i1 x$ L1 S5 h0 ]
上述每一个变换对应于蕨类植物的一部分。第一个变换被选中的概率最大,因此被执行的次数最多,从而产生了蕨类植物的茎和底部的叶子。第二个和第三个变换分别对应于左边和右边底部的叶子,第四个变换绘制了蕨类植物的茎。 $ z8 y9 z1 k$ q( T$ ^
这是一个非均匀概率选择的例子,我们在第五章中已经学习过,以下程序为指定的点数绘制Barnsley蕨类植物。 , d" R3 l' U; w8 E9 m
Draw a Barnsley Fern5 K: @$ M% X! e& Q
$ \* ~0 t) h- N9 g9 w( q4 ? import random
$ Q- R- \5 Q) ^' B) _: n: s import matplotlib.pyplot as plt& V% r' s T" `* a& h9 z0 m! g8 z
def transformation_1(p):
8 e4 x2 W. V$ O4 x x = p[0]) b3 K3 f' L! b' u! V: O
y = p[1]
: V& L# e; o) |$ n" O. z9 N x1 = 0.85*x + 0.04*y
4 f) k4 @6 E* L) t) N' j, L4 ] y1 = -0.04*y + 0.85*y + 1.6
- y# M) D7 W4 Y# S- H return x1, y1) h# E) f0 N$ ?$ i0 F
def transformation_2(p):
. e9 ]9 F6 K n' {# e4 U& D x = p[0]9 S) ~4 l4 i4 U- O
y = p[1]2 O0 b4 q4 F2 T Z
x1 = 0.2*x - 0.26*y% I% K+ g8 r% {
y1 = 0.23*y + 0.22*y + 1.6, O: f! y- a; U T9 `7 g s
return x1, y1
, W5 M$ L' D" D3 ~+ o! t0 J def transformation_3(p): u" ^& O% @/ _$ y5 q
x = p[0]
2 w, c* ~! R$ z& \* i' o& X9 T y = p[1]+ Q. o3 Y" ^2 G9 D) P. Y2 R
x1 = -0.15*x + 0.28*y
( S w7 r7 G' _ y- c y1 = 0.26*y + 0.24*y + 0.44+ C2 d% u* W3 f' c9 ~
return x1, y1
* B/ t2 t. g' z% W; k! T1 N def transformation_4(p):5 i1 d/ b8 w- }
x = p[0]
; R- n: H) F: l4 U4 P4 z" _ y = p[1], Y O3 q2 C3 h1 F4 A1 K2 X
x1 = 0' i6 F% ~: d% T ~ C* U5 B' e
y1 = 0.16*y5 u6 K* H* F) j; w# I
return x1, y1
) l& |3 D( Z6 L. i$ S( b def get_index(probability):% e& c# t2 A3 {2 z+ x# |! n
r = random.random()
4 G$ t' Q$ i. e4 y% j) m. l6 T/ F c_probability = 0
3 z+ z+ {$ U. L/ `! N' h" P sum_probability = []- D& t' B9 H# [- u- c4 M% g
for p in probability: t5 ?+ T# v7 I
c_probability += p0 x7 D$ o, x5 N
sum_probability.append(c_probability)
* P1 i7 d% x* I) c. l' v8 F for item, sp in enumerate(sum_probability):0 f9 Y* Q6 ?) p' ~: S+ E: b: \
if r < sp:9 e$ S9 E, G! {: \
return item
( N( O4 K L- y9 Z1 r3 u0 U return len(probability) - 1! h P( \: Z: h
5 P. x" C5 B) B" L O def transform(p):
6 \: ^8 d0 X( u # List of transformation functions4 i! |% d7 a$ `, \
transformation = [transformation_1, transformation_2, transformation_3, transformation_4]: x; A# n3 J& @8 x* b
probability = [0.85, 0.07, 0.07, 0.01]
. Y. V8 W7 L* T# k+ B # Pick a random transformation function and call it0 {. H' H! \" s; }3 }9 b' J1 ~7 S
tindex = get_index(probability)
' ~7 r/ ]6 d' z t = transformation[tindex]
4 N d3 K( a. X/ r, ~0 e) E x, y = t(p)6 o F* \( Q- n- y1 B# Q7 [
return x, y
$ O- I% b0 ?. k: ^ def draw_fern(n):
$ l0 ?" M' v3 K/ y8 i # We start with (0,0)
% Y2 p( S3 Y' c6 O x = [0]6 e3 {7 J& z7 `6 K! f% P- E
y = [0]
' a' m( w1 v* z x1, y1 = 0, 0( A9 O3 K+ I3 @- Y
for i in range(n):& r: w# ]$ \1 |1 [$ W1 j) ^
x1, y1 = transform((x1, y1)), n% v) @0 a# m" {9 a: ?7 l" B
x.append(x1): D3 j8 M7 n# a4 r1 Q
y.append(y1)
' D3 ~( k4 |- [$ P+ v return x, y" {: M3 z( R1 G$ w+ l
if __name__ == __main__:
: H' K$ X8 N: }* M2 _! o n = int(input(Enter the number of points in the Ferns: ))
) [, J* b$ a& P( A x, y = draw_fern(n)
: b! h$ E3 U, I( A plt.plot(x, y, o)
( [" J2 t4 f4 N) x4 U: q+ G7 C, [, i plt.title(Fern with {0} points.format(n))
( s! l9 M2 P, {4 D plt.show(); d/ N& |/ Z7 J8 p$ Q( A3 o3 U" x& P- L
运行此程序,他首先询问蕨类植物图中指定的点数,然后开始绘制该图。下面两张图分别展示了具有1000个点和10000个点的蕨类植物图。 3 t$ i: V0 Y2 z$ D/ p$ E, X
 ; X1 {5 \* j+ y" {) C: s9 O ; X1 {5 \* j+ y" {) C: s9 O
制定了1000个点的蕨类植物叶片 , W9 m& J. Q, R# T) b' L
 . ^' i8 @( a; K
. ^' i8 @( a; K 指定了10000个点的蕨类植物叶片
' S4 f& Y3 n. o& Y, J6 q 这4个变换规则分别在transformation_1(),transformation_2(),transformation_3(),transformation_4()函数中定义。get_index()函数返回按照给定概率下的一种随机变化的索引值,这个概率我们之前已经讲过了,不清楚的可以返回去在第五章非均匀概率那里再次学习。返回索引之后即可选择某一个具体的变换来应用。
2 L0 E" t" I# H# c4 L! [; K 初始点(0,0)变换的次数即为程序输入中指定的蕨类植物点的个数。 1 F3 e( i! z7 `0 @' I
: X$ o/ \ i! D& Y( _& A& B
, D8 ` Y. Y0 h$ Z/ H
' Z& {. ^5 }6 N4 K
. y6 c2 e! g5 }" \ |


