matlab中基于传递函数或者状态方程的幅频特性分析

已知传递函数，求出幅频特性。

随便举一个传递函数为

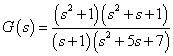
在matlab中写入代码如下。

代码有两种写法，一种是直接写传递函数G 的表达式，简单粗暴。tf 其实就是transfer  function的缩写，即传递函数。

[C] 纯文本查看 复制代码

s=tf('s');

G=(s^2+1)*(s^2+s+1)/((s+1)*(s^2+5*s+7));

bode(G);

grid

xlabel('频率f');title('   ');

另一种写代码的方法：

[C] 纯文本查看 复制代码

num=conv([1,0,1],[1,1,1]);

den=conv([1,1],[1,5,7]);

bode(tf(num,den));

grid

xlabel('频率f');title('   ');

这里conv命令就是将分子分母的因式乘出来，然后按照s的幂次降序得到num 和den 两个一维矩阵，num=[1,1,2,1,1]，den=[1,6,12,7]。再直观一点说，这时候

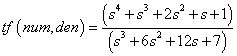
此时，tf (num, den) 和第一种中的G就是等价的。运行得：

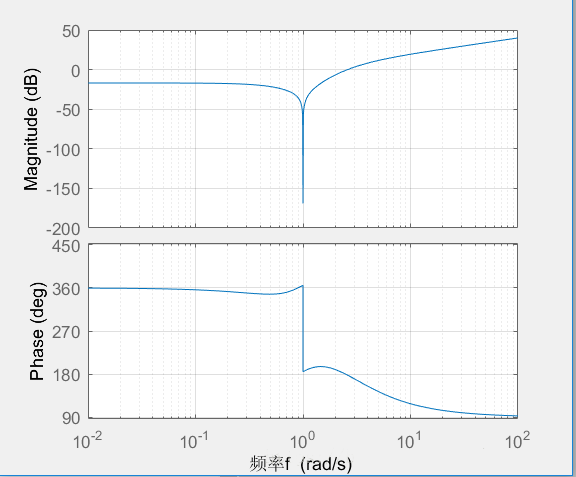
有的时候我们不需要bode图中的相角图，只想要频率图，只需要将bode(G) 换成

[C] 纯文本查看 复制代码

h = bodeplot(G);

setoptions(h,'FreqUnits','Hz','PhaseVisible','off');

得出来：

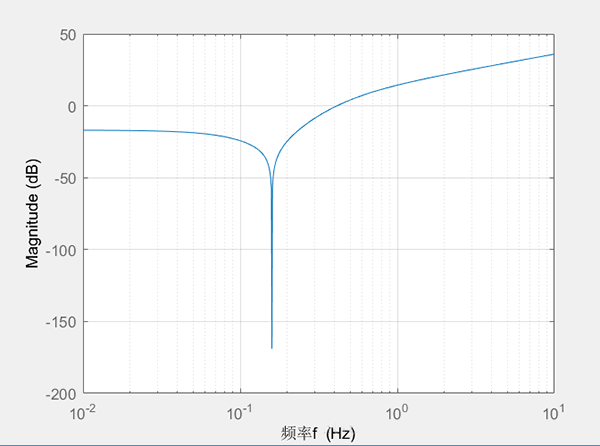
2

已知状态方程，求幅频特性

对于一般的状态方程

传递函数G=Y/U。

[C] 纯文本查看 复制代码

[num,den]=ss2tf(A,B,C,D)

这里求出的num 和den与上述的一样，只不过此时的传递函数就取决于你所设定的Y有几个输出量了，如果Y有三个量，那么，num和den将会是三维矩阵，对应着三个传递函数，剩下的工作就和上面的一样了。

至于将传递函数转成状态方程，就是上面的逆过程 [A,B,C,D]=tf2ss(num,den)。不过我目前还没用到，因为我觉得根据自己所需要的状态变量最后得出的状态方程会不一样，用matlab中求出的状态空间只是其中一种。

原文链接：

游客，如果您要查看本帖隐藏内容请回复

' |' y& j/ N0 l) i
; I! F  b8 X2 [# D