2022年诺贝尔物理学奖正解：量子纠缠和贝尔不等式的原理与实验 | 韩锋

　　10月4号重阳节下午，科学网以直播形式播放了2022年诺贝尔物理学奖的发布现场。斯德哥尔摩的瑞典皇家科学院宣布，将2022年诺贝尔物理学奖授予法国物理学家阿斯佩克特（Alain Aspect）、美国实验和理论物理学家克劳泽（John F. Clauser）和奥地利科学家泽林格尔（Anton Zeilinger），以表彰他们“用纠缠光子进行的实验，确立了贝尔不等式的违反，并开创了量子信息科学”（for experiments with entangled photons,establishing the violation of Bell inequalities and pioneering quantum information science）。

% G5 \7 }1 o( j+ s( Y& L

　　阿斯派克特、克劳泽和泽林格尔的工作，通过对“贝尔实验”的分析，证实和阐释量子现象的独特性质——非定域性和量子远程关联的纠缠态，也决定性地否定了玻姆隐变量的存在，肯定了现有量子力学理论的正确性，所以意义深远。它对进一步肯定和加深对量子力学的理解，发展在量子信息，尤其是量子通信和量子计算方面的应用，更是有着广阔的前景。

　　1.量子现象中的非定域远距离关联

}% ~: d2 B' Q

　　关于非定域远距离关联，指的是这样一件事情。考察粒子(光子或电子等)通过双狭缝后在屏上形成的干涉花样，当堵住一个缝而让粒子只通过另一个缝时，干涉花样将立即变为衍射花样。可以设想，如果这两个缝相距相当远，它们之间是类空间隔（即它们之间不可能交换信息而实现因果联系），一个缝被堵住的信息是如何瞬时地传达到另一个狭缝处的呢？如果确有信号在它们之间传递，那是违背相对论的定域因果性原则的。

" _5 T G) `. m! \

　　问题的严格表述要从所谓EPR论证(或EPR佯谬)说起。1935年，爱因斯坦和波多耳斯基 (B. Podolsky)、罗森(N. Rosen)共同发表了一篇题为“能认为量子力学对物理实在的描述是完备的吗?”的文章（见许良英等编译《爱因斯坦文集》(第一卷），商务印书馆（1976）：328-335），认为：如果现今的量子力学是正确（自洽）的，那么它就一定是不完备的，因为理论中没有完全包括物理实在的每一个元素所对应的物理量（测不准关系，或称“不确定度关系”）。

7 v% B+ {, W1 ?

　　当然，要辩明这一问题，首先得明确定义到底什么样的理论才算是“完备”的？EPR（爱因斯坦、波多耳斯基、罗森三个人姓名的首字母）认为：如果物理实在的每一个要素都在物理理论中有它的对应量，那么这个理论就是完备的。而如果对物理系统不作任何干扰，就能确定地预言一个物理量的值，那么这个物理量就是物理实在的要素。换句话说，客观实在性与人们的观测无关。

. e" r0 J* }$ x7 N8 J( B$ ^3 }3 z

　　另外，还须认定满足相对论的定域性原则，即自然界不存在超距作用，没有超光速信号。EPR论证大致上是这样的：为简单起见，假定现在有一个动量为零的复合粒子系统，在t = 0到t = T这段时间分裂为两个粒子Ⅰ和Ⅱ，在T时刻已远离不再有相互作用。现在测量Ⅰ的动量为P，根据量子力学中仍然有效的动量守恒定律，对Ⅱ不用进行测量就可以知道它的动量是-P，因而Ⅱ的动量是物理实在的一个要素。另一方面，测量Ⅰ的坐标，根据复合系统的波函数，又可以对Ⅱ不加测量地预示为，因而Ⅱ的坐标也是物理实在的一个要素。如果量子力学理论是正确的，测不准关系成立，Ⅱ就不能同时具有确定的坐标和动量。由于坐标和动量都是可以观察度量的物理实在的要素，因而一个完整的理论二者皆应包容其中。根据理论的完备性判据，物理实在的所有要素现在在量子力学中并不同时都有对应量，而且这与测量无关。因而，量子力学是不完备的。

　　电子的双缝干涉实验：电子和所有微观粒子一样都具有波粒二象性。当一群电子（或者一个一个电子多次发射）通过双狭缝时，电子将携带着概率波的信息，以波的形式通过双缝，在屏幕上形成电子数密集分布的干涉条纹。

　　上文发表后不久，玻尔便迅速地作出了反应。为了加强针对性，他以同样的标题撰文反驳。其要点是不同意EPR的实在性判据，即认为不可能有无干扰的测量。物理量本来就是和测量仪器、条件与方法紧密联系着的。任何量子测量的结果使我们得到的并不只是对象客体的信息，而且包含着关于这个客体浸没在其中的实验环境的整体信息。观测者的实验意图、实验安排、实验手段等，这些也可被认为是一种“干扰”，它不单要干扰Ⅰ，还要影响Ⅱ。测量对象和测量仪器、测量手段共同构成了一个不可分割的整体。两个曾经相互作用过的粒子Ⅰ和Ⅱ是相互关联着的一个不可分割的整体，即使它们分离得再远也将仍然是不可分离地相互关联着的。对第Ⅰ个粒子的测量不造成对第Ⅱ个粒子影响的前提是不成立的。系统的这种整体性量子关联是基本的，而把系统看作是由彼此可以分离、并加以单独描写的部分所组成的观点则只能是一种经典近似。这就从根本上改变了关于整体和部分相互关系的观念。由于在这里不存在关于信号传递的问题，因而它与相对论中的定域性原则相矛盾的问题也就不存在了。

　　然而，量子力学的统计特征总让人感到有些不自在，使人们难以彻底接受。玻姆(David Joseph Bohm)等人的隐变量理论就是企图在量子领域消除统计性而恢复单值决定论的一种努力（关于玻姆的隐变量理论，可以参考洪定国《物理学理论的结构与拓展》，科学出版社（1988）：§4.2,-4，-5，-6）。隐变量理论认为，在深一层次中，对单个系统的测量不存在测不准关系，它只是一种量子涨落的统计结果。隐变量理论对于远距离关联的解释是：两粒子的隐变量彼此有联系，它们通过这种内禀性质携带着指示它们到达给定仪器时应如何行动的信息，而在不同的实验装置中有不同的行动。这里不存在观测对象与测量仪器之间不可控制的相互作用。

　　为了将是否存在定域隐变量的问题付诸实验以做出判定，贝尔 （John Stewart  Bell）从隐变量存在的假定出发，根据可分离原则，导出了一个两粒子自旋系统的不等式，即贝尔不等式（出自他1964年的论文“On the Einstein Podolsky Rosen Paradox”）。比如讨论一个由两个光子或电子那样的粒子1和2所组成的总自旋角动量为零的单态系统。当它们向相反方向飞出很远时，由于角动量守恒，第1个粒子如果是右旋偏振的，那么第2个粒子也将不受影响还是右旋偏振的（这句话是怎么回事？一个是右旋，另一个不应该是左旋吗？还有为什么要说不受影响？）。当然也可以把它们分解成线偏振态的叠加，实际上有时测量线偏振态可能更方便一些。由此导出了遵从隐变量理论的贝尔不等式，其原始形式为：︳P(a,b) - P(a,c)︱≤ 1 + P(b,c),式中P(a,b)称为粒子1和粒子2的“自旋关联” 函数，它的定义是：粒子1沿单位矢量a方向的自旋分量 与粒子2沿单位矢量b方向的自旋分量二者测量值之积的统计平均值。作同样的理解。他证明了，量子力学的“自旋关联”是与贝尔不等式矛盾的。换句话说，一个定域隐变量理论不能复现量子力学的结果(这被称为“贝尔定理”)。要么贝尔不等式正确，要么量子力学正确，二者必居其一。

　　自1972年以来已经做过的十五个以上的实验中，只有早期(1973，1974)两个实验是和贝尔不等式一致的，而且其可靠性尚有疑问。也就是说，非常倾向于否决定域隐变量理论存在的可能性，而肯定量子力学的正确性。

$ Y$ I2 q; k5 [$ s* p" B

* j3 w F$ j5 g' f, }, d# P+ U

　　两个电子组成的总自旋角动量为零的系统：无论它们相距多远，始终是一个统一的整体。比如，当这边电子的自旋状态由于测量从原来的不确定变为向上时，那边电子的自旋状态就瞬时地从原来的不确定变为向下。这种远程关联并没有发生相互作用的信号传递，所以不存在所谓“超光速”的问题。

　　2.量子现象中的纠缠态

　　量子现象中的纠缠态来自于量子力学中的态叠加原理。比如有名的“薛定谔猫态”就是这样的纠缠态，这是薛定谔在1935年提出的一个思想实验。他设想：将一只猫关在一个装有放射性物质的铁箱子里，放射性物质的强度小到比如1小时只有一个原子核发生衰变而放射出一个粒子，也可能不衰变而不放射粒子，两者的概率各为50%。如果一个粒子被发射，它将触发继电器松开一把小锤子，击碎一个装有氢氰酸毒药的小瓶子而毒杀这只猫。当然，如果没有粒子被发射，猫就会安然无恙活得好好的。将这个箱子搁置1小时，不打开箱子，问：这只猫是活的还是已经死了？如果这只猫的状态可以用一个波函数形式来描述（当然，在这里宏观物体的状态能不能用波函数来描述，也还是个问题，不过因为这只是一个假想的思想实验，所以也就不用考虑这个问题了），那么这个波函数所描述的就是一个死活各有一半概率的叠加态。这样的叠加态，也就是我们常说的“纠缠态”。

9 i; E, Y e1 V5 z7 i

　　在我们未打开箱子观察之前，这只猫是活的还是死的? 它当然不会既是活的又是死的。在观测之前，猫处于死活各占一半的叠加态，观测行为将使概率坍缩，而以相等的可能性落在猫活着或死了的本征态之一上。有人设想，如果把箱壁做成是透明的如何？则按量子力学，连续地观测放射性原子核，就是对它施加了作用，它就可能永远也不衰变，因而猫也就一直不会死去，这是由于箱壁透明时的观测实际上是照明用的光子与放射性核的相互作用改变了核衰变的几率特性的结果（这常称为“量子芝诺效应”）。

; A0 L J2 g @7 h, b+ `6 N n+ v

1 I" `" a+ w+ G& u$ _ D

　　 量子芝诺效应：当单个电子通过双狭缝时，在屏幕上将打出一个光点，重复多次，大量电子的光点将在屏幕上形成明暗相间的干涉条纹。可是，如果想用探测器观察电子究竟是通过哪个缝的，屏幕上的干涉条纹将立即消失，成为直对狭缝的两条光带。这让人感到非常诡异，这等于是说“如果盯着看烧开水，水就永远不开。”其实，这个现象再好不过地说明了：在量子现象中，那种完全不受观测影响（或者说“干扰”）的物理实在是不存在的。

　　且不说无人观察时的猫处于一种死活难以区分的不确定状态这一点很难让人接受，观测行为竟然能以相等的可能性决定猫的死活这一点更难让人接受。其实，日常生活中的猫这一宏观物体，总是处在同环境的相互作用之中，这种相互作用已不可避免地会使其叠加态坍缩为单一态，这种坍缩与对它何时进行观测显然无关。可见，薛定谔猫的状态不是被观测所改变的，而是被相互作用改变的，人的观测只是让这种结果显示了出来而已。处于纠缠态的系统，它里面的所有子系统都是相互关联着的，或者说里面的子系统是作为一个整体的一部分存在的，无论它们相距多远，只要其中的一个子系统发生变化，那么其它的所有子系统都会跟着发生变化，这就是量子现象的整体性特征。这里并没有信息传送的问题，所以根本不存在超不超光速的问题。如果说它是什么超光速现象的超距作用，违背了相对论中的光速不变原理，那完全是误读。

7 P( U& e c- Y+ j! v3 g

　　薛定谔猫态：图示描述猫的波函数是一个活态和死态各有一半概率的叠加态，观测将使波函数发生坍缩，坍缩到对观测者呈现出来的那个本征态

5 B) `: |" n: m( |

　　3.贝尔不等式的实验检验

　　自从1964年贝尔提出贝尔不等式以后，物理学家们终于找到了可以判断隐变量理论和量子力学究竟谁正确的标准。从1972年到1982年间，陆续进行了许多检验贝尔不等式的实验。在这些实验的结果中，绝大多数的可靠的结果都与量子力学的预言相一致——即贝尔不等式不成立，基本上可以断言定域隐变量理论不存在。不过，那些贝尔不等式的检验实验在实际上也都还存在着不少的“漏洞”，由于在实验中所用的粒子对、分析器和检验器等还存在一定的缺点。正是由于有漏洞的存在，定域隐变量理论的支持者们坚持认为该理论并没有完全被排除。

　　下面来介绍实验中排除漏洞的方法。阿斯派克特小组在进行实验的时候巧妙地设计了一个随机切换开关，它可以使偏振分析器的方向在光子离开源之后可以切换。让两个检偏镜距离纠缠源分别大约6米左右。因此，当两个光子快到检偏镜的那一刻，它们的距离大约是12米。最快的信息传递速度是光速，光也需要40纳秒的时间来走完12米的路程。他们使用的设备，能使得检偏镜在每20纳秒的时间内旋转一次。这样在一个光子从检偏器的一端传播到另一端之前，检偏镜已经做了旋转，两个纠缠光子就不能有足够的时间来相互通知对方。

　　阿斯派克特实验满足爱因斯坦的定域性条件，即：“要求两个粒子的关联测量的选择在每一个分析器上都是完全独立的。尤其是，当一个测量进行时，人们必须保证在两个分析器之间没有通信。……这指的是，两个检测事件所要求的时间必须短于从一个分析器/检测器传播到另一个的时间。”该实验结果同量子力学的预言一致。因此，这个实验被认为已经封闭了定域性漏洞，从而得到大多数学者的肯定。

6 U% O: w+ z* W2 u- e* N" \

　　但是，泽林格尔对阿斯派克特实验尚有一些异议。他认为阿斯派克特实验还有一个致命的弱点，那就是开关的切换不是随机的，而是准周期的，在参数上也有重合。换句话说，该实验还不能完全封闭定域性漏洞。阿斯派克特关于这个实验的论文中就曾指出：“我们以大于L/C的速度改变偏振器的方向。因为这种改变并不是真正随机的，而是准周期的，因此理想的方案并没有完成。为了反驳遵循爱因斯坦隐参量的理论，一个具有完全随机开关的更加理想的实验是必要的。”

0 W5 X1 o1 l4 m; l6 Q

　　定域性隐变量是否存在的实验关键，就从定域性漏洞是否完全封闭转到了检偏器是否是随机转动的问题。于是实验中检偏器是否能够随机的转动成了实验的最为关键的环节。基于这个考虑，泽林格尔等人进行了更为完善的实验。1998年魏斯（G. Weihs）,杰纳维恩（T. Jennewien）,西蒙（C. Simon）,韦恩福特尔（H. Weinfuter）和泽林格尔在《物理评论快报》上发表了“严格爱因斯坦定域条件下贝尔不等式的违反” [Phys. Rev. Lett, 1998(81): 5039-5043]的论文。他们所完成的这个实验，在相关的文献中常被称为泽林格尔实验。

) x; F+ Q5 X9 ]7 [' t- K$ F

　　泽林格尔实验使用参量下转换（PDC：parametric down-conversion）技术来产生纠缠光子对，如图所示（以下图象取自 A. Zeilinger，et al. An experimental test of non-local realism. Nature. 2007, 446: 873-874）图中，从泵浦激光器中产生的激光脉冲，通过一个2毫米厚的非线性晶体产生纠缠光子对。光子对分别经过二分之一玻片和厚度为前面二分之一的非线性晶体补偿后，经过偏振分析器。之后光子再经过滤光器后，分别落在两个计数器上A = ±1和B = ±1方向上，利用庞加莱球来记录有关数据。其中，右边线路中插入四分之一玻片是为了调节不同的角度差，以便于进行多次测量。     

. v( _ J+ ^% f( B; ]' \0 d! I

　　实验装置图示

# a- _# r2 ~$ Q# w% s c

　　实验的结果如下图a 所示。图a标绘了对非定域隐变量理论（NLHV）的不同角度时，实验值及隐变量理论值、量子力学理论值的变化情况。从图中可以看出，当时，实验值和量子力学理论值符合的很好，而与隐变量理论值则偏离较大，且在时偏离最大。

. d- m% M: u. O# ~1 E$ `

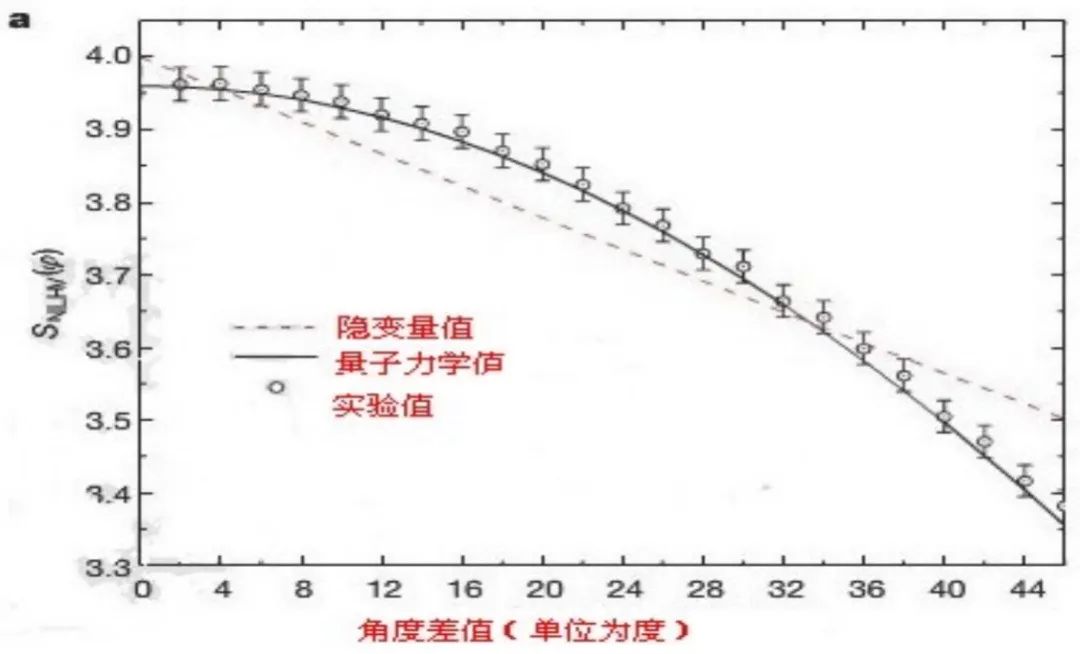 图a  检验隐变量理论实验坐标图

　　（原来Bell理论所提供的不等式在实验上很难检验，因此克劳泽等人在1969年提出了一个与之等价但在实验上更友好的CHSH不等式，C就是克劳泽姓名的首字母。对贝尔不等式的实际检测，一般用的就是CHSH不等式。）

1 e9 J* k- N; `6 F# o

　　下面图b标绘了在不同角度时，实验值及贝尔- CHSH不等式值、量子力学理论值的变化情况。从图中可以看出，时实验值与量子力学理论值符合的很好，远超出贝尔不等式的限制，在时实验值超出此值最多。在泽林格尔实验中有一个非常重要的改进，使用了一种真正的物理随机数发生器，以克服阿斯派克特实验所留下的缺憾。        

4 f& M: }- G) S/ u' y* U& Q4 q

2 x; h( O0 m& X# P% y2 W

　　图b  检验贝尔不等式实验坐标图

　　4.几个需要澄清的问题

. c7 ?8 Z& \* Y6 f# @' F

　　①为了通俗地说清楚什么是量子纠缠，很多人用打比方的方式来说明，这当然也未尝不可。其中最常用的就是那个“手套”比喻，即当我手上的这个盒子里的手套如果是左手，那一定可以肯定远处的那个盒子里的手套一定是右手。但是这里有个“坑”需要注意，那就是：如果这也算“纠缠”的话（姑且可以称它为“经典纠缠”），它与“量子纠缠”还不是一码事。其区别在于：经典纠缠中，那个远处手套的右手，和你手中手套的左手都是确定的。而在量子纠缠中，两个“手套”的状态，在没有打开盒子观测之前都并不确定，而是只有一定的概率（比如各有50%）取某个值。只有当你进行了观测，使你手中的“手套”坍缩成为“左手”，那远处的“手套”就自动由于“纠缠”而成为“右手”，这才是量子纠缠。

' o$ S+ x0 K6 O1 A7 {

　　②关于定域性：狭义相对论否定了牛顿经典力学的超距作用，认为一个物体对另一个远处物体的作用，是通过场传递过去的，是需要时间的。由于真空中的光速是自然界最快的速度，所以相互作用传递最快的速度也就是光速，瞬时的或者超光速的相互作用是不存在的。一个物体对远在30万公里之外的物体发生相互作用，最短也需要1秒钟时间。如果那个物体在40万公里处，在1秒钟时间是不可能对它发生作用的。这就叫做“定域性”。在量子现象中，如果总自旋为零的双粒子系统中的两个粒子相距甚远，比如有40万公里，如果它们处于量子纠缠态，那么这里粒子的状态一旦发生变化（比如测量自旋从不确定变为向上），远处的那个粒子的自旋就会瞬时地从不确定变为向下（由于角动量守恒），不需要时间。这种情况如果是真的，那显然是违反“定域性”原则的。这看起来与狭义相对论直接矛盾，所以爱因斯坦称它为“鬼魅般的超距作用”，认为那是绝对不可能的。但事实上，由于测量的结果不能事先确定，量子纠缠并不传递信息，所以并不存在什么“超光速”违反狭义相对论的问题。

5 P" m5 w- g% E* t

　　③关于“整体性原则”：整体性特征是量子现象所特有的，是一种既区别于经典物理，也区别于相对论的性质。正因为量子现象具有整体性，所以才有了量子纠缠。由于处于纠缠态的粒子并不是通过相互作用而关联的，那个粒子的行为并不是由于这个粒子对它的作用而发生改变的，它们之间并不存在那种由于相互作用而发生的因果关系，所以也就不存在什么“超距作用”的问题。狭义相对论的“光速不变原理”仍然成立，真空中光速是自然界相互作用传递的最大速度这一点也仍然正确，相对论的定域性原则仍然有效，这一切都没有任何变化。只有在量子现象中才会有量子纠缠，这是需要明确分清的。

　　④关于贝尔不等式：约翰·贝尔本来是相信爱因斯坦相对论的定域性的，认为量子力学的非定域性量子纠缠可能有问题。在爱因斯坦的EPR佯谬提出以后，他导出一个不等式（贝尔不等式）的目的，是想通过用实验来证实这个不等式，肯定定域性而否定非定域的远距离关联，即量子纠缠的可能性。然而，实验的结果却事与愿违，大量的越来越精确的、堵塞了越来越多漏洞的实验都否定了这个不等式，也就是肯定了量子力学没有问题，那种认为量子力学的底层还有一个满足定域性的“隐变量理论”的观点并不成立。正确的表述应该是：实验判定了贝尔不等式不成立，从而现有的量子力学理论是正确的。贝尔不等式只是一个判据，大量的实验目的是通过贝尔不等式的检验来肯定或否定量子力学，贝尔不等式本身不存在正确与否的问题。

) R6 i! C) ?; s1 Q% E2 A

　　⑤爱因斯坦所持的那种实在论，即物理实在的每一个要素都应该在物理理论中有它的对应量而完全与测量无关，以及玻姆等人的那种试图摆脱量子概率性的定域隐变量理论，是否存在？还有，是不是只有决定论的因果性，概率论的非决定论是不是也是一种因果性？这本来都是一些理解量子现象的基本哲学问题。贝尔不等式及其检验，是将一个基本的哲学问题，通过数学的演绎论证，转化成为一个可以通过实验来解决的物理问题，这是一个重大的创举，有着深远的意义和深刻的内涵。可以预期，将来可能会有更多的在哲学上有争议的问题，通过数学处理，转化成为可以通过实验判定的问题，那将是哲学研究的一大进展。

　　韩锋

, G& C+ l. \. c7 a

　　笔名（也是网名）雪塵，男，汉族，山西文水人

0 @& C! N q |* V! r2 V

　　新疆师范大学物理学教授，广西河池学院兼职教授、“科学与人文研究中心”主任，广西师范大学兼职硕士复旦大学物理系理论物理专业研修学者，北京大学科学与社会研究中心访问学者

0 E# W: D( Z7 Y2 O; [

　　中国自然辩证法研究会、中国天文学会、新疆物理学会、新疆教育学会等学术团体的会员或常务理事

1 y' X' O f' \5 V" ?- } $ J" @" L6 Q: m + D8 v! H+ o. K# K \. G 9 m- A$ g5 u$ L" o4 P ! k2 F9 ]4 n z# B) Y8 E 2 r: H" P$ `9 g& I' n. i, H