|
( m8 _+ a1 O; m8 n3 m
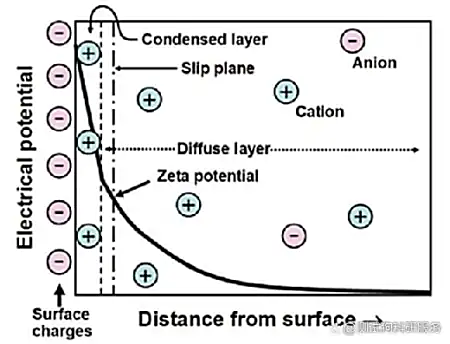
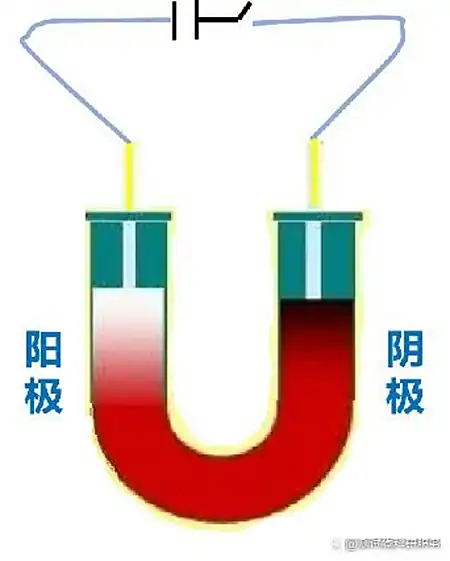
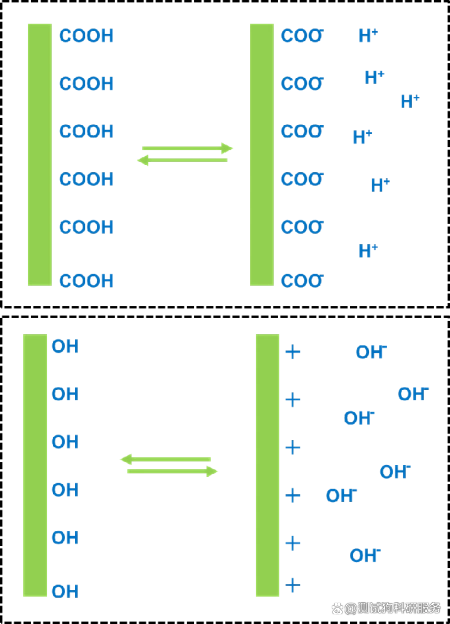
1.引言在纳米科学领域,Zeta电位是一个非常重要的概念,它是对颗粒之间相互排斥或吸引力的强度的度量。根据Zeta电位,我们能够详细了解分子或颗粒的分散机理,这对静电分散控制至关重要。Zeta电位可用于测定分散体系颗粒物的固-液界面电性(电位),可用于测量乳状液液滴的界面电性,也可用于测定等电点、研究界面反应过程的机理。通过测定颗粒的Zeta电位,求出等电点,是认识颗粒表面电性的重要方法,在颗粒表面处理中也是重要的手段。目前,Zeta电位的测量广泛应用于化妆品、选矿、造纸、医疗卫生、建筑材料、超细材料、环境保护、海洋化学等行业,同时,Zeta电位也是化学、化工、医学、建材等领域的重要理化参数之一。2.Zeta电位的基本理论要真正的弄清楚Zeta电位的基本原理,首先需要理解一下双电层理论。那什么是双电层呢?我们知道,热运动使液相中的离子趋于均匀分布,带电表面则排斥同号离子并将反离子吸引至表面附近,溶液中离子的分布情况由上述两种相对抗的作用的相对大小决定。根据斯特恩的观点,一部分反离子由于电性吸引或非电性的特性吸引作用(例如范德瓦耳斯力)而和表面紧密结合,构成吸附层(或称斯特恩层)。其余的离子则扩散地分布在溶液中,构成双电层的扩散层。由于带电表面的吸引作用,在扩散层中反离子的浓度远大于同号离子,离表面越远,过剩的反离子越少,直至在溶液内部反离子的浓度与同号离子相等。如图1所示,最左侧的“surface charges”可看成分散在水中的固体粒子的表面电荷。悬浮在水中的粒子,其表面的带电基团总是倾向于吸引溶液中带相反电荷的离子(即"反离子")。但所有的离子都具有热能,所以它们会不停地运动。所以离子一方面在静电作用下被吸引到粒子表面,另一方面在热扩散的作用下远离粒子表面,这两种作用的净效果是所有离子在颗粒表面获得某种平衡分布,这种平衡分布也就是形成了离子云。值得注意的是,图中有一层反离子被画成与粒子表面直接接触,即它们处于所谓的紧密层(Condensed layer)中,而另外的反离子被画成是扩散的,即处于所谓的扩散层(Diffuse layer)中。紧密层和扩散层相接的地方存在一个滑移层(处于距离紧密层朝外方向很短的地方),大致地我们可以这样认为:粒子在水中运动的时候,滑移层左侧的离子都能跟随粒子一起运动,而其右侧的粒子则没有那么"死心塌地"地跟它走,所以两者之间会产生滑动。在此处,Zeta电位指的就是水相中固体粒子的滑动面相对于远处(即离子平衡处)的电位(Electrical potential),这个电位通过仪器是可以实际测到的。图1双电层模型示意图因此,纳米颗粒本身带不带电荷或者带什么电荷并不重要,重要的是,如果Zeta电位仪检测得到的是正值,就说明纳米颗粒整体表现出来的是正电荷,我们称之为纳米颗粒表面带正电;如果Zeta电位仪检测得到的是负值,就说明纳米颗粒整体表现出来的是负电荷,我们称之为纳米颗粒表面带负电荷。此外,Zeta电位的重要意义在于它的数值与胶态分散的稳定性相关。如图2所示,清晰的揭示了Zeta电位的大小与体系稳定性之间的大致关系。Zeta电位是对颗粒之间相互排斥或吸引力的强度的度量。分子或分散粒子越小,Zeta电位的绝对值(正或负)越高,体系越稳定,即溶解或分散可以抵抗聚集。反之,Zeta电位(正或负)越低,越倾向于凝结或凝聚,即吸引力超过了排斥力,分散被破坏而发生凝结或凝聚。图2 Zeta电位与体系稳定性的关系3.Zeta电位的测试方法经过长时间的探索发展,目前测量Zeta电位的方法主要包括电泳法、电渗法、流动电位法和流动电流法等,下面笔者将对其进行展开介绍。3.1电泳法电泳法是将待测液注入两端加有电压的电泳池中,然后用激光多普勒测速法测量胶体粒子迁移速度,再根据Zeta电位和移动速率的关系,从而计算出待测溶液的Zeta电位。那么,什么是电泳呢?所谓电泳,是带电粒子在外电场的作用下相对于其悬浮液体(例如,水)产生运动的现象。再简单讲,就是在液体样品两端加了外电场之后,液体中带正电的粒子会朝外电场的负极移动,带负电的粒子会朝外电场的正极移动。如图3所示,带正电的氢氧化铁胶体,经过一段时间的电泳,负极段的颜色就会深。图3 Fe(OH)3胶体的电泳现象对于电泳法,目前最常见的测试仪器是基于多普勒电泳光散射原理的Zeta电位仪,它利用多普勒电泳光散射原理,通过测量光的频率或相位的变化间接测出颗粒的电泳速度。这类Zeta电位仪主要由激光源、衰减器、样品室、检测器、数字信号处理器、相关器和计算机等组成,其基本工作原理见图4。首先,激光通过电子束分裂器分成基准光束和入射光束,其中基准光为多普勒效应提供参考光束,入射光则通过衰减器进入样品室。当光束照到运动的颗粒时,就会引起光束频率或相位发生变化,检测器将此信号传送到数字信号处理器和相关器,进而传送到计算机。图4多普勒电泳光散射Zeta电位仪的结构对纤维或填料表面的Zeta电位的检测是其最常见的应用之一,故而为了使介绍更为清晰明了,笔者以此为例来说明Zeta电位测量中的流动电位法。如图5所示,是其基本的工作方式。图中该仪器利用真空将纤维悬浮液吸向滤网而在滤网上形成纤维垫,然后测定装置于纤维垫两端的一对电极之间的电位差(筛网本身常常被用作其中一个电极)。纤维垫两侧施加一定真空压时的电位值与不施加真空压时的参考电位值进行对比。图5纤维表面Zeta电位测量示意图3.4流动电流法流动电流法的基本原理是:在机械外力的作用下,待测液沿毛细管壁流动,而扩散层的反离子随待测液一起流动,并在管的一端聚集,通过测量该过程中形成的流动电流得到Zeta电位。该信号非常微弱,通常利用放大装置对电流信号进行放大,然后经过同步整流器和灵敏度调整,测得流动电流信号,因而后续的信号处理具有一定的复杂性。4.Zeta电位的影响因素Zeta电位具有如此重要的意义,然而在许多情况下,一些胶体粒子的电动行为并没有像经典电动理论所预测的那样,随着离子强度的增加,Zeta电位的绝对值持续下降,此外还存在利用不同的实验技术测得的同一物质的Zeta电位也不同的情况。基于此,笔者从内因和外因的角度分别总结了Zeta电位测量过程中的影响因素。4.1内因影响Zeta电位的内因主要指分散体系本身的性质对Zeta电位的影响。pH:影响Zeta电位最重要的因素是pH,当谈论Zeta电位时,pH是不可忽视的因素。 Zeta电位对pH作图在低pH将是正的,在高pH将是负的,这中间一定有一点会通过零Zeta电位,这一点称为等电点,是相当重要的一点,通常在这一点胶体是最不稳定的。如图6所示,在悬浮液中有一个带负电的颗粒,往这一悬浮液中加入碱性物质,颗粒会得到更多的负电;但若往这一悬浮液中加入酸性物质,在一定程度时,颗粒的电荷将会被中和;进一步加入酸,颗粒将会带更多的正电。图6纳米颗粒表面电荷来源电导率:双电层的厚度与溶液中的离子浓度有关,可根据介质的离子强度进行计算,离子强度越高,双电层愈压缩同,离子的化合价也会影响双单层的厚度,例如三价离子(Al3+)将会比单价离子(Na+)更多的压缩双电层。无机离子可有两种方法与带电表面相作用:对于等电点没有影响的非选择性吸附和会改变等电点的选择性吸附。即使很低浓度的选择性吸附离子,也会对Zeta电位有很大的影响,有时选择性吸附离子甚至会造成颗粒从带负电变成带正电,从带正电变成带负电。此外,样品中的不同添加剂浓度对样品的Zeta电位也会产生很大的影响,研究样品中的添加剂浓度对产品Zeta电位的影响可为研发稳定配方的产品提供有用的信息,研究样品中已知杂质对Zeta电位的影响可作为研制抗絮凝的产品的有力工具。4.2外因影响Zeta电位的外因主要指一些外在的干扰,比如人为因素或Zeta电位仪的精度对Zeta电位的影响等。电渗运动:影响测量精度的主要因素,它与电泳运动方向相反,极大地影响电泳速度测量的真实性。因此,测量时必须有效地剔除由于电渗运动所引起的误差。根据胶体化学的有关论述,只有当测量在所谓“稳定层”上进行时,体系的电渗运动速度才可为零,理论上,这时得到的结果才是电泳运动的速度。交叉污染:由于Zeta电位对于体系的离子环境十分敏感,因此交叉污染对于电化学测量的影响巨大。样品池和电极若清洗不干净,其表面带有残留电荷后,容易吸附样品,并增大引入样品交叉污染的可能性。展宽:Zeta电位的测量实际上就是对体系电泳运动速度的测量。这个过程中,样品颗粒电泳率不均匀所造成的非均匀性拓宽以及由于颗粒布朗运动速度与电泳运动速度叠加所造成的扩散拓宽,都会造成多普勒频移线拓宽,进而降低测量分辨率,影响测量结果的精度。信噪比与温度变化:高信噪比是仪器高性能的根本保证,其中激光器功率大小就是一个关键的影响因素。对于低电泳迁移率或极稀体系的样品,低功率激光器在测量时产生的低散射强度会使系统的信噪比降低,影响测量结果的可靠性。温度变化会引起某些体系粘度以及布朗运动剧烈程度的变化,进而影响Zeta电位的测量结果。5.应用分析正如前面提到的,Zeta电位的测量使我们能够详细了解分散机理,因而其在酿造、陶瓷、制药、药品、矿物处理和水处理等各个行业应用广泛。目前,包括艾滋病毒在内的病毒性疾病的传播治疗是一个紧迫的问题,在当今医学中用于治疗免疫缺陷疾病的药物普遍具有合成复杂以及副作用多的问题。因此,人们对来自天然来源(植物来源)的化合物(包括多酚)作为合成抗病毒药物的替代品这一途径非常感兴趣。而其中,单宁属于植物的次生代谢产物,具有多种生物活性,包括抗病毒活性。Szymon[1]等人研究了人血清白蛋白(HSA)与两种鞣花单宁的相互作用,发现将单宁添加到蛋白质中会导致Zeta电位略有增加(图7)。值得注意的是,在实验误差范围内,没有研究单宁和有研究单宁的HSA的Zeta电位值是相同的,说明在研究化合物的存在下,人血清白蛋白表面结构无明显变化,保持稳定。这项工作揭示了Zeta电位分析在药物领域的应用。图7加入单宁时HAS的Zeta电位膜技术现已广泛应用于各种工业应用中,包括水净化,制药,生物技术,石化和纺织等。膜的一般作用是从各种溶液中分离,纯化,浓缩或去除物质,例如微生物,细颗粒,蛋白质,核酸,糖,其他有机物和矿物溶质。膜表面的电荷效应较为复杂,对电荷行为的详细检查可提供对溶质-溶液-表面机理相互作用的更多了解,从而可以更好地理解后续的膜工艺性能。Matthew[2]等人研发了一种全新的测定膜表面Zeta电位的方法,用于测量超滤,纳滤和反渗透膜的表面电荷。如图8所示,使用切向流电势和激光多普勒电泳评估了PTFE膜的Zeta电位。可以看到,PTFE膜在低pH范围内带正电,然后随着pH的增加而迅速变为负,等电点在pH 为5左右。在较高的pH值(7.5)下,膜的Zeta电位稳定在约-20 mV。该工作证实了激光多普勒电泳是通过确定膜表面Zeta电位来表征膜表面电荷的合适方法。与传统方法论相比,该技术具有多个优势,其将方法扩展到覆盖带正电的表面,这使该新技术能够跨越膜表面电荷表征所需的整个测量范围。图8未改性PTFE膜的Zeta电势6.参考文献[1] Szymon Sekowski, Ewa Olchowik-Grabarek, Weronika Wieckowska, Artem Veiko, Lukasz Oldak, Ewa Gorodkiewicz, Eduard Karamov, Nodira Abdulladjanova, Saidmukhtar Mavlyanov, Elena Lapshina, Ilya B. Zavodnik, Maria Zamaraeva. Spectroscopic, Zeta-potential and Surface Plasmon Resonance analysis of interaction between potential anti-HIV tannins with different flexibility and human serum albumin, Colloids and Surfaces B: Biointerfaces,2020,194,111175.[2] Matthew Walters, Saif Al Aani, Peter P. Esteban, Paul M. Williams, Darren L. Oatley-Radcliffe. Laser Doppler electrophoresis and electro-osmotic flow mapping for the zeta potential measurement of positively charged membrane surfaces, Chemical Engineering Research and Design,2020.159,458-476.
# }5 t1 V2 ]6 {- f! ~* n: Y
- z2 ]& n8 \8 f9 l% W% z4 [ 9 ~5 O: n) F9 R9 r1 _4 p
 " ^# Y7 U: ]1 m7 F " ^# Y7 U: ]1 m7 F
* s1 d* [- u6 h2 S+ I
8 w. ?+ M& j# i& x7 F1 P. o( V7 _. P
! _' w& B( l5 t4 m+ x, ]$ B- P' x
, i# H. m9 N1 A$ E7 _! e$ Q  5 ^2 e7 j( l& O1 {" L0 ~
5 ^2 e7 j( l& O1 {" L0 ~ - v1 W* Z3 q2 O6 W1 y
9 t$ d, O T( [: x5 w' J& w
' g! ~" z9 _( U5 |3 r 2 f4 K. t2 } {/ {$ p4 |" V
 b# A" t- y1 W, Y; u7 L& z b# A" t- y1 W, Y; u7 L& z
7 u" M; l- k( n, F8 B6 L 0 u& K* v3 l' a0 ~3 b: F
9 N# { E7 O7 p* {% t) E6 p& K
6 r# p' L3 H5 ?2 C5 S  ! G& B3 H* a9 a$ N ! G& B3 H* a9 a$ N
4 N3 x- Y8 {$ H5 `' c Y ? + K- G3 F4 c4 E9 T& u. X7 H
8 r H7 Y3 ]6 q+ b" U6 O
" A6 }( ]1 ~( y; F" Z  0 q: q: J( E& e
0 q: q: J( E& e : c, M3 P% g- v- J) s
* l8 a5 R1 K" A# O! e2 ]# u
- v$ B3 F' z9 {, d) k6 Y
`/ ~: i) d+ ~" M& y! e  4 P w+ s, B( D 4 P w+ s, B( D
# i7 A" {7 s3 t* c4 P! @
5 i, h2 e/ \/ i4 P" ?$ P
0 u5 C/ F0 z: i; \5 [( y
( s0 ?6 j8 Y7 y b1 J7 h% | 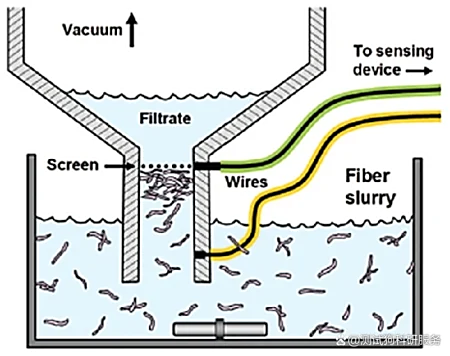 $ X& e' c" L/ J" e. T
$ X& e' c" L/ J" e. T ! u0 F% I# P! B$ p% E
+ b7 ^% L9 a3 L
% ~, ^* r9 }) w5 X9 ?
7 ^7 g: }) y, m* M
 5 e8 q; K2 ~% g$ f2 n1 @- u4 P 5 e8 q; K2 ~% g$ f2 n1 @- u4 P
% u P# o4 J4 T" j# [
/ j# t2 x% E. G8 X9 \# @, b0 N$ y * z% d: b9 u2 {5 \ J% Y5 D- d
% X3 }/ Y+ o T" Q5 i( E
 2 \2 o3 o. }/ P' \6 H7 ] 2 \2 o3 o. }/ P' \6 H7 ]
- l9 C! r% H2 V" ]
# p! n- F+ ?' p8 ~* J 0 s' ]/ N% N1 x J
* D z3 Q8 Y2 V0 `# ]( d/ o 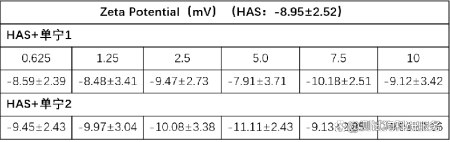 * P, M1 n( y( g/ m * P, M1 n( y( g/ m
- T3 K2 K) j: T, G / H" l( l5 {" [& {
8 F6 m p" m9 {0 O) T
' `7 ^+ ]( A9 k6 M6 A/ S2 g 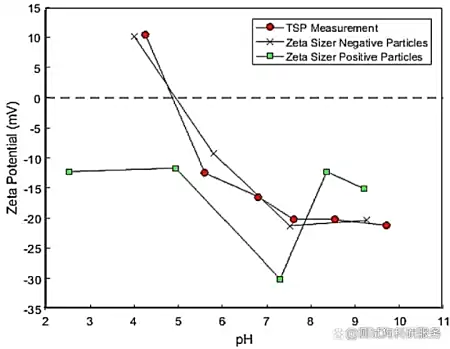 : I7 | S5 u# C$ n5 |0 V, K
: I7 | S5 u# C$ n5 |0 V, K + D5 S* s% F( p$ R
- ~$ M* y; a5 j2 P; b
0 P4 c# z( O8 I, `' B
& p% o4 x" [5 C: ^& h1 V2 _
: {6 ] s( ?7 O1 `8 r4 q
, K9 ~5 P {9 d, Q
5 I3 t5 b; I; |+ O |


