论文专区▏差分技术在海洋测量中的应用 - 什么是海洋测量技术

【编者按】文章系统分析了差分概念在无线电定位、卫星定位、平均海面和深度基准面传递、水位改正、重力场和磁场向下延拓等方面的应用模式。差分技术在卫星导航定位中的应用非常普遍，在海洋测量中举一反三，还可以推广到更多的应用领域，有效消除系统误差，解决很多的实际问题，提高信息获取与处理精度，或者降低问题的复杂性。本文发表在《海洋测绘》2017年第1期上，现编发给朋友们阅读了解。翟国君，男，1961年出生，山西临汾人，高级工程师，博士，博士生导师，主要从事海底地形测量和海洋大地测量技术与应用研究。

+ V S K6 ?+ c: ^ ]$ S

文/翟国君 黄谟涛 欧阳永忠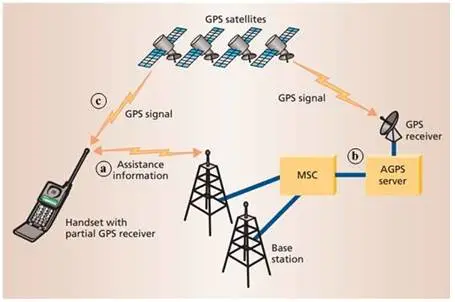

" L( K0 F: H0 c+ J0 P8 @/ ^; x

一、引言

差分的概念由来已久，尤其在卫星定位应用方面，先后出现了按观测量区分的坐标差分、伪距差分、相位差分、相位平滑伪距差分等等，此外还可按数据处理的方法，将差分GNSS分为单站差分GNSS、区域性差分GNSS和广域差分GNSS等。依据基准站所处的位置，又可分为岸基差分、星站差分等[1-2]。差分技术的应用大大提高了卫星定位的精度，在海洋测量方面得到了广泛的应用。

$ l' U# P7 D% D& _! q6 ` [9 W

其实，差分的概念除了在卫星定位方面的应用外，在海洋测量的其他方面也有很多应用，只是术语不同或者没有特别强调差分二字而没有引起大家的关注。这里，对差分概念在海洋测量方面的应用进行梳理分析，通过与不同的专业领域相结合，将会开发出更多的类似应用。

二、差分技术在海洋测量中的应用模式

⒈ 导航定位中的应用

⑴无线电导航定位中的应用

- T ?! `2 H0 S1 D* m$ B

无线电定位方式有测距（圆-圆）定位和距离差（双曲线）定位。这里以双曲线定位为例。双曲线无线电定位系统是根据一个动点相对两固定点（双曲线的）的距离差保持不变，这个动点的轨迹为一条双曲线的原理而设计的一种定位系统。有两条双曲线时，即可交会出船的位置[3]。

距离差是由船台接收三个岸台发来的无线电信号，并分别测量它们的相位差来求得的。即：

D0－D1＝λ(Δφ1/2π)           ⑴

, c# A& h/ d# U

D0－D1＝λ(Δφ2/2π)           ⑵

对于脉冲相位双曲线中远程导航定位系统罗兰-C而言，是通过测量时差来进行双曲线定位的。即：

D0－D1＝(T1－ε1) c/a      ⑶

% x% g0 J R+ B

D0－D1＝(T1－ε1) c/a      ⑷

为了提高罗兰-C在某一海域的定位精度，可采用差分罗兰-C的方法。也就是将罗兰-C监测接收机固定于需要改善定位精度的海域内，用监测接收机测量出时间偏差。再根据所在位置上预先获得的长期的平均时间差，得到测量区域附近的测量时差的改正量，将该改正量发给附近海域的测量船，由船台对接收机时间差的读数进行修正。经过这种修正后，即可大幅提高定位精度。即：

9 v' H2 a& Q6 E# z& e

D0－D1＝(T1－Δt1－ε1) c/a          ⑸

, }' z) v0 o g$ a7 [' N

D0－D1＝(T2－Δt2－ε2) c/a          ⑹

⑵卫星导航定位中的应用

; V I* M3 `+ [$ Q0 g

卫星定位作为一种全天时、全天候、全球覆盖的高精度定位系统在海洋测量领域得到了广泛的应用。利用GNSS信号进行测量定位时，由于卫星定位信号受到星历误差、星钟误差、电离层和对流层时延改正误差、多路径误差、观测噪声误差以及天线相位误差等各种误差源的影响，使得常规的单点定位精度较低。尽管其中的一些系统性误差可以通过模型加以削弱，但对很多应用来说其残差仍是不可忽略的。为了提高GNSS的定位精度，出现了GNSS相对定位，也就是差分GNSS定位，其定位精度可以轻松达到厘米级，甚至毫米级[1-2]。对于一定区域内的两个定位点而言，除了星历误差和星钟误差这类共有的误差之外，还有一些误差对于两个定位点来说其影响基本相同。比如，电离层和对流层对两个距离比较近的定位点而言，其误差的影响具有很强的相关性，距离比较近时，可认为它们对于两个定位点的影响是相同的。根据这一基本概念，可以用两台GNSS接收机，分别安置在位于陆地的基准站上和位于船上的流动站上（当然基准站和流动站也可以都位于陆地上），同步观测相同的卫星，从而实现差分定位。

1 ~% r8 @* E- V4 R9 n3 Q

①坐标差分

+ w! l5 P! K2 ?

在GNSS定位初期，当对定位点的精度要求不高时，可以认为各种误差对A站的影响与对B站的影响相同。即认为基准站坐标的真值（已知值）与观测值之差等同于流动站坐标的真值与观测值之差。

$ F& F5 Z" I% S# q/ @

图1  GNSS差分示意图

设基准站的坐标真值为(XA,YA,ZA)，事先通过高精度定位手段获得。基准站的坐标观测值为(XA′,YA′,ZA′)，由GNSS定位得到。

, o- O% _$ L6 s9 D( S+ `% ]/ l9 e

流动站的坐标真值为(XB,YB,ZB)，待求。流动站的坐标观测值为(XB′,YB′,ZB′)，由GNSS定位得到。

, h# Z2 h2 y1 c! q+ V9 r

﹛ΔX＝XA－XA¹

/ V: m5 t! A- l- @

﹛ΔY＝YA－YA¹           ⑺

5 k$ l$ r, Q0 U; {4 P. _

﹛ΔZ＝ZA－ZA¹

流动站接收机既测定自己的三维坐标，又接收来自基准站接收机的位置改正值(ΔX,ΔY,ΔZ),而用后者改正自己所测得的三维坐标(XB`,YB`,ZB`)则有：

8 T$ x: C7 ~( r5 @; o1 ]

﹛XB＝XB`＋ΔX

﹛YB＝YB`＋ΔY          ⑻

﹛ZB＝ZB`＋ΔZ

* T2 W3 a4 \$ g* [8 \0 S) @& D

当进行坐标差分时，基准站只需要向流动站用户发送三个差分数据，即三个坐标改正数（ΔX,ΔY,ΔZ）即可。实践表明，当基准站接收机和流动站接收机之间的距离在100km以内时，坐标差分能够显著提高流动站用户的位置精度。

②伪距差分

9 K4 T1 G/ F3 a* R5 G

伪距差分是用基准站伪距校正量校正流动站伪距的一种GNSS差分定位方法。利用伪距差分定位技术可以大大减弱基准站和流动站的公共误差，如卫星星历误差、大气传播延迟误差及星钟误差等。在基准站上事先利用已知的基准站坐标和卫星坐标求出基准站到卫星的距离，然后将其与接收机测量的伪距进行比对，求出伪距改正数及其变率，然后将所有卫星的伪距改正数及其变率传输到流动站，流动站利用此伪距改正数及其变率改正相应的伪距，解算出流动站的精确坐标。

设基准站r与卫星j之间在时刻的伪距为ρr´(t)，基准站与卫星的理论距离为ρr0´(t)，则伪距与理论距离之间的差值为：

Δρr´(t)＝ρr´(t)－ρr0´(t)          ⑼

. U# [6 P8 I6 z+ p, C. Q

流动站k接收机收到此伪距改正数，加上自身测量的伪距，即可得到经过改正的伪距为：

& H9 Z {, ?2 J6 Z! F

ρr0´(t)＝ρk´(t)－Δρr´(t)          ⑽

流动站接收机在测量伪距的同时，接收来自基准站接收机的伪距改正量，用于改正它自己测得的伪距，这一做法的前提条件是基准站与流动站之间的距离比较近，可以认为星历误差和大气传播延迟误差对两个站的影响是相同的。

3 `. F1 |- m) T, b

③相位差分

- b( Z) Y& E9 ]' R' I% i! v3 U5 N

相位差分是一种用基准站和流动站载波相位观测量组成差分的高精度GNSS定位方式。由于相位测量精度高，利用相位差分定位可以大大减弱卫星星历误差、大气传播延迟误差、星钟误差和站钟误差。载波相位差分测量与微距差分测量的主要差别是，前者的差分数据为载波相位校正值，而后者的差分数据为伪距的校正值。

! m9 H& i( `" b- r6 d

设基准站接收机所测得的载波滞后相位为：

ρrj(t)＝λNjr＋λCjr(t)＋φjr(t)

% }9 `8 |" D$ d' l; z. u

＝ρn´(t)＋Ajr(t)λ/f＋C [dtjr(t)－dTr(t)]            ⑾

式中，各符号的含义此处从略。

根据基准站r的已知三维坐标和第j颗GNSS卫星在时元t的在轨位置，可算得基准站r到第j颗GNSS卫星在时元t的真实距离ρn´(t)，进而可求得GNSS载波相位测量的校正值：

ρr´(t)－[λNjr＋λCjr(t)＋φjr(t)]＝Δφjr(t)

＝－Ajr(t)λ/f－C [dtjr(t)－dTr(t)]           ⑿

' t5 ]& [, [( P1 T& F

流动站k接收机所测得的载波滞后相位为：

ρkj(t)＝λNjk＋λCjk(t)＋φjk(t)

＝ρjkt(t)＋Ajk(t)λ/f＋C [dtjk(t)－dTk(t)]    ⒀

$ E. C9 J7 l; o2 B8 o4 j7 t

流动站接收机同时接收基准站发来的GNSS载波相位测量校正值Δφjr(t)，用于改正它所测得的载波延迟相位，即有：

ρjkt(t)＝ρjk(t)－Δφjr(t)         ⒁

只要流动站接收机和基准站接收机均观测了4颗以上的在视GNSS卫星，就可解算出流动站用户的三维位置。

, i, s6 J/ o! p; N( d5 ]

⒉ 水位控制技术中的应用

' ?2 p- }, B, s1 c5 O9 y

⑴平均海面传递中的应用

平均海面是海洋测绘中一个重要的界面。一方面它近似代表了地球的形状，另一方面，它是深度基准面起算的参考面。尤其是多年平均海面，在海洋测量中的地位更加重要。众所周知，多年平均海面是由验潮站多年的观测资料计算得到。但是，现实中不可能在海洋区域以理想的密度布设验潮站进行潮汐观测，另外在很多情况下，有些验潮站的观测时间长度不够，无法利用其验潮资料计算得到多年平均海面。这时候就可以利用具有差分意义的平均海面传递技术来达到确定多年平均海面的目的[4]。下面以平均海面的同步传递法为例加以说明。

假设验潮站A为长期验潮站，验潮站B为短期验潮站。平均海面传递的基本原理如图所示，其实质就是假定短期平均海面与长期（多年）平均海面的差值在验潮站A和验潮站B是相同的。

图2  平均海面传递示意图

验潮站A为长期验潮站，用MSL表示长期平均海面，M表示短期平均海面。令：

ΔB＝MSLB－MB         ⒂

ΔA＝MSLA－MA        ⒃

假设：

ΔB＝ΔA

从而可确定验潮站B的长期（多年）平均海面为：

7 H5 v; \1 ]/ A+ M' Z0 i

MSLB＝MB＋ΔB＝MB＋ΔA＝MB＋MSLB－MA      ⒄

; \+ V4 c9 n& c7 }* |# I/ l* ?

由此便实现了长期（多年）平均海面从长期验潮站A到短期验潮站B的传递。

⑵深度基准面传递中的应用

与平均海面一样，深度基准面同样也存在着传递的问题。在短期验潮站和临时验潮站上，因为验潮时间短而无法像长期验潮站那样按照规范要求计算深度基准面，只能采用传递的方法加以解决[4]。下面以同步改正法传递深度基准面为例加以说明。

: e$ ~0 y% {; V" g8 p

图3 深度基准面传递示意图

假定验潮站A为长期验潮站，验潮站B为短期验潮站。带有下标0的L表示从验潮站零点起算的深度基准面值。令：

ΔB＝MB－LB0        ⒅

Q5 o6 m4 s+ v6 i! x

ΔA＝MA－LA0        ⒆

8 T. j/ S1 L& B

假设

% }) Q6 k7 J! \' q' K+ ~4 X

ΔB＝ΔA

从而可确定验潮站B从水尺零点起算的深度基准面为：

% |1 _$ P; ]5 N/ k( P2 J

LB0＝MB－ΔB＝MB－ΔA＝MB＋LA0－MA      ⒇

$ z/ M% y9 A1 O

验潮站B从多年平均海面起算的深度基准面可由下式得到：

- S5 g$ x) J- _# Y

LB＝MSLB－LB0

MSLB是验潮站B的多年平均海面，可由平均海面传递的方法得到。

( V7 W5 D+ `5 p% R) `

由此便实现了深度基准面从长期验潮站A到短期验潮站B的传递。

) [" p8 D! a5 }1 U

⑶余水位改正中的应用

* j( w% i, G- m9 G6 d

余水位改正法是最近十多年才出现的新的水位改正方法。其基本原理是，将水位分解为潮位和余水位（非潮汐水位），在此基础上利用潮波模型和余水位监测值实现测区任一点的水位恢复。在把水位划分为潮位和异常水位（余水位）的前提下，可对二者实行单独的空间内插处理。潮波（也即潮高）的空间内插主要由其动力机制决定，在有高分辨率潮汐场模型的情况下，该问题将自动得到解决。异常水位的传播特征则复杂得多，但在小范围（100km左右尺度）内，其传播特征会有明显的规律性，主要表现为空间相关性与时间相关性[5-7]。

某点的实际水位为潮位与异常水位之和，若在测区中某点a未进行直接的水位观测，其潮汐参数已知(通过以往观测或潮汐场模型得到)，则可根据潮汐表达式方便地计算潮高，根据余水位的空间分布和时间上的近似一致性，通过一个或多个设站处的实测数据与预报数据的差表示所求点的异常水位，比如在已知点b有：

. X& D2 x# j/ V L( U" I# v/ G* K: g

ΔSb(t)＝hb(t)－Tb(t)           (22)

式中，ΔSb(t)为b的余水位，hb(t)为b的实际水位，Tb(t)为b的预报水位。

根据两个站余水位在空间和时间上的强相关性，可近似认为：

ΔSa(t)＝ΔSb(t) (23)

$ q8 Y3 M% \; h( b$ r5 E2 J+ x

于是：

$ x6 e/ J2 n4 n% x( g* _

ha(t)＝Ta(t)＋ΔSb(t)

从而获得a点的实际水位。

⒊ 重磁信息延拓处理中的应用

⑴航空重力延拓中的应用

航空重力测量向下延拓一直以来备受关注。由于重力场向下延拓过程在数学上属于不适定反问题，因此向下延拓的的不稳定性是客观存在的。很多学者就重力场的向下延拓问题进行了深入的研究，提出了不同的解决办法。文献[8]为了克服上述问题提出了一种海域重力场向下延拓的实用方法，体现了差分这一概念的应用。

这里以利用卫星测高重力向上延拓直接计算延拓改正数，从而实现航空重力测量向下延拓归算的方法为例。

6 d) t1 r, l' @. o

设由卫星测高反演得到的海面重力异常为Δg0卫，对应一定高度上的空中重力异常为Δgp卫，则根据Poisson积分方程得：

# q* t c) T4 z2 I* Q/ E3 @" l

式中，（rp,φp,λp）表示空中计算点的三维坐标；（r0,φ0,λ0）代表海面流动点的三维坐标；ρ为计算点与流动点之间的空间距离。因为向上延拓计算过程是稳定收敛的，所以无论是采用传统的离散化求和法，还是采用现代的FFT技术，求解式（25）总能给出可靠的向上延拓结果。按上式求得空中重力异常Δgp卫以后，可进一步按下式计算向下延拓改正数[8]：

2 r3 e. m y- h

δΔgp0卫＝Δg0卫－Δgp卫                     (26)

8 h6 x, b5 d) B6 ?" ^) t

将δΔgp0卫近似作为航空重力测量向下延拓的改正数δΔgp0航，即可按下式完成航空重力测量数据的向下延拓计算：

+ S+ M9 F6 x3 E/ E2 g

δΔgp0航＝δΔgp0卫

Δgp0航＝Δgp航＋δΔgp0航＝Δgp航＋Δgp0卫          (27)

本方法的基本思想就是在假设δΔgp0航＝δΔgp0卫的情况下，实现了航空重力的向下延拓。

1 Z$ l6 s! j; O0 _( i& J

⑵航空磁力延拓中的应用

; t. k8 c! C* L

同航空重力测量一样，航空磁力测量向下延拓也是人们长期以来不断研究的课题。从物理意义上讲，磁力场向下延拓一样存在着不稳定性[9-14]。按照海域重力场向下延拓的实用做法，这里假定地磁场模型具有高阶次高精度的特点，进而即可提出海域磁场向下延拓的实用方法，体现了差分这一概念的应用。需要说明的是，目前地磁场模型还不像重力场模型具有那么高的阶次和精度，该方法还只能是理论意义上的。

4 r" C7 g6 F* C' \( @( K" t. C

设由高阶次地磁场模型计算得到的海面磁力异常为ΔT0模，对应一定高度上的空中磁力异常为ΔTp模，则可进一步按下式计算向下延拓改正数：

δΔTp0模＝ΔT0模－ΔTp模             (28)

. W' Q3 w7 p: Y* o( F$ h+ p

将δΔTp0模近似作为航空磁力测量向下延拓的改正数δΔTp0航，即可按下式完成航空磁力测量数据的向下延拓计算：

δΔTp0航＝δΔTp0模

* Q5 e3 I2 i. P: u& m

ΔT0航＝ΔTp航＋δΔTp0航＝ΔTp航＋δΔTp0模         （29）

y$ R, F4 z5 V* c7 u1 {4 x

本方法的基本思想就是在假设δΔTp0航＝δΔTp0模的情况下，实现了航空磁力的向下延拓。

# v: V. F4 D3 a A, O0 X N! e$ p

三、讨论与结论

$ Q9 }8 g$ D, m& \$ m6 j- d

虽然在不同的专业领域差分技术的应用形式不同，但其应用前提必然是该差分改正量对于基准站（基准面，已知站，固定点，等等）和流动站（待求站，待求量，等等）在空间上、时间上、相位上，或者某种其他的环境里有着很强的相关性。正是基于这种相关性，差分技术在某种程度上消弱了共同的系统误差，简化了复杂问题的求解。

即使对于简单的应用而言，比如单站水位改正的以点代面、声速剖面改正的以站代区、地磁日变改正的以台代区等，无不体现了差分的概念。

对于复杂的应用而言，比如卫星导航定位中的伪距差分、相位差分等，更加体现了差分改正量在空间和时间上的相关性，差分后的定位结果大大消弱了电离层误差、对流层误差、钟差等共有的误差影响。不论是局域差分、广域差分、星站差分，还是网络RTK、PPP、CORS站技术，都是差分技术广泛而有效的应用。

利用卫星测高数据反演重力场方面，目前普遍采用的方法是利用逆维宁曼尼兹公式进行反演。在利用平均海面高求取垂线偏差时，实际上计算的就是海面高的一次差分，这种做法大大消弱了平均海面中的长波长误差，提高了重力异常的反演精度。

差分概念在海洋测量相关领域应用较广，合适的应用可以取得意想不到的效果。差分概念的某些应用可以大大提高结果的精度，有的应用则可以大大简化问题的复杂性。基于差分概念的应用，尽管某种程度上存在一定的近似，但有一点是共同的，那就是改正量在某种环境里、空间上、时间上、相位上存在很强的相关性。这一相关性在卫星定位的差分应用和基于余水位的测深水位改正应用方面体现的尤为明显。基于这种时空上的相关性，就可以结合某个专业领域开发出更为广泛的应用。

参考文献：

% m. P w0 o) |% p

[1]党亚民,秘金钟,成英燕.全球导航卫星系统原理与应用[M].北京:测绘出版社,2007.

[2]刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2005.

$ E6 s l( o% m9 E

[3]彭光宇,赵明才.海洋测量定位与计算[M].北京:测绘出版社,1993.

[4]刘雁春.海洋测深空间结构及其数据处理[M].北京:测绘出版社,2003.

[5]黄辰虎,卫国兵,翟国君,等.海道测量中余水位分离方法的研究[J].海洋测绘,2013,33(6):5-10.

[6]裴文斌,牛桂芝,董海军.余水位及潮汐差分方法[J].水道港口,2007,28(6):439-443.

. n/ {2 m2 s2 _# W9 @

[7]唐岩,暴景阳,许军.余水位的内插及其对潮高模型的精化[J].测绘科学,2007,32(6):94-95.

, t* r0 H5 o1 I

[8]黄谟涛,欧阳永忠,刘敏,等.海域航空重力测量数据向下延拓的实用方法[J].武汉大学学报,2014,39(10):1147-1152.

+ j& C1 t6 q2 Y! T

[9]徐世浙.位场延拓的积分-迭代法[J].地球物理学报,2006,49(4):1176-1182.

[10]于波,翟国君,刘雁春,等.噪声对磁场向下延拓迭代法的计算误差影响分析[J].地球物理学报,2009,52(8):2182-2188.

5 s* `. e! o7 N0 x7 q' t& }

[11]于波,翟国君,刘雁春,等.利用航磁数据向下延拓得到海面磁场的方法,测绘学报,2009,38(3):202-209.

1 j5 p# X p8 ~% b- M7 J

[12]翟国君,卞光浪,王克平.利用改进泰勒级数法对磁异常场进行向下延拓[J],海洋测绘,2012,32(4):17-21.

[13]卞光浪,翟国君,高金耀等.总强度磁场稳健向下延拓的改进泰勒级数法[J].测绘学报,2014,43(1):30-36.

* v5 [, @4 N7 } h4 j! C

[14]陈龙伟,徐世浙,胡小平,等.位场向下延拓的迭代的最小二乘法[J].地球物理学进展,2011,26(3):894-901.

■论文专区的文章均为在《海洋测绘》上刊发的论文，若其他公众平台转载，请备注论文作者，并说明文章来源，版权归《海洋测绘》所有。

$ n, W# w2 U2 H$ Z& x) F: Q" | i

相关阅读推荐：

8 W6 d, I! W7 J+ v: |

论文专区▏国际海道测量服务与技术标准进展研究

测绘论坛▏GPS测高技术在无验潮海洋深度测量中的应用

论文专区▏多波束无验潮水深测量中垂直基准模型构建

海测讲坛▏暴景阳：海洋（测绘）垂直基准建设思考

0 e: B* k1 z) f

科普▏大地测量系统和参考框架

论文专区▏GNSS多系统组合精密定位研究进展

投稿邮箱：452218808@qq.com，请您在留言中标注为投稿，并提供个人简介及联系方式，谢谢！

# q# N1 c% E( V6 i3 s, ~' E