|
6 @% C5 y1 b) v! d( C

: ]5 K! u! O }& t1 G' r' f" `/ i8 w 点击图片上方蓝色字体“慧天地”即可订阅 ( n1 d4 ?- ~5 N; `

$ Y0 d, K6 Y9 \4 U+ E, _ 英文原文来源:www.gislounge.com 0 a+ C% Z! L6 E2 c J7 i
中文编译整理:慧天地国际站一鸣,版权归原作者及刊载媒体所有。
) W$ L" O' f! o6 Y2 q 征集第十三届中国智慧城市大会优秀应用成果案例,详情请点击链接:
- {7 X4 I }' [ 关于征集第十三届中国智慧城市大会优秀应用成果案例的通知
+ i) ]* h. p: X) z 自19世纪以来,Voronoi图在理解空间模式和特定现象的显示方面得到了普及,它们被用于绘制伦敦霍乱疫情的地图。这些图的思想是它们是由一个点生成的凸多边形,并且生成点比其他多边形点更接近其多边形点。这些多边形表示一个平面在一定距离内的区域的划分。每个分区称为一个单元格。不同形式的镶嵌细分定义了不同类型的多边形布局。Voronoi图也称为Thiessen多边形,通常使用Delaunay准则来进行计算[1]。 ( S; i( ]. G' {$ {7 J9 N1 c
早期在流行病学中使用地图是许多地理信息系统教科书和课程中的一个热点例子,以突出地理分析的应用。 ' z7 r& a2 Y6 {& p
使用GIS创建Voronoi图的挑战
0 g, v; z5 E9 ?# t5 {1 J5 x 虽然有基于栅格和矢量的方法来定义Voronoi图,但是基于矢量的方法对于面积保持来说往往更加复杂。因此,通常使用基于栅格的方法来定义镶嵌细分[2]。Voronoi图,因为它们是基于将如何对其他多边形进行细分,所以计算机可能需要很长时间。因此,并行算法和分布式计算方法被应用于大面积复杂的镶嵌[3]。在地理信息系统和空间方法的Voronoi研究中已经解决的挑战性问题中包括了为地球表面创建复杂的Voronoi形状,其中复杂的表面几何结构造成了运行过程的复杂性。距离变换方法可以用来计算陆地表面之间的距离,从而使镶嵌成为可能。然而,这种方法往往会导致某种程度的误差,因为必须估计距离,计算可能需要很长时间才能生成给定的镶嵌。而栅格分辨率可用于确定所需的精度水平,在这种情况下,镶嵌可以容忍一定程度上的错误[4]。 ' A- I/ y9 y. s2 e
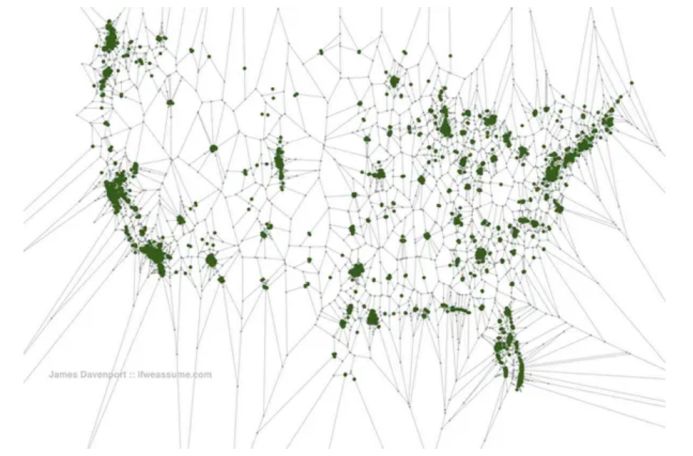
% o* d/ w$ |$ J5 b" K
图1:展示每个星巴克位置的Voronoi图(图片来源:JAMES DAVENPORT)
$ W- y! [1 O$ t% X% Q" X' K0 \' V Voronoi镶嵌的应用
+ c$ I" d7 ~: w; K: J 至于相关方向的应用,Voronoi镶嵌已经在各种情况下被使用。在最近的研究中,一个应用是确定中国某个省份里与学校教育相关的社会经济关系。在这种情况下,使用所谓的晶体生长镶嵌(crystal-growth tessellation)来表示一种加权方法,将连续的社会经济数据划分为离散的原点[5]。其他研究Voronoi的方法包括使用三维地理信息系统来更好地规划安保摄像机的放置方式。人们可以通过Voronoi计算来优化需要放置摄像头的位置,以便其完全捕获三维空间,然后通过摄像机的位置进行测试,这可以衡量算法在多大程度上定义了用于观察的Voronoi空间[6]。 7 I6 k' E" k6 U w' q, g
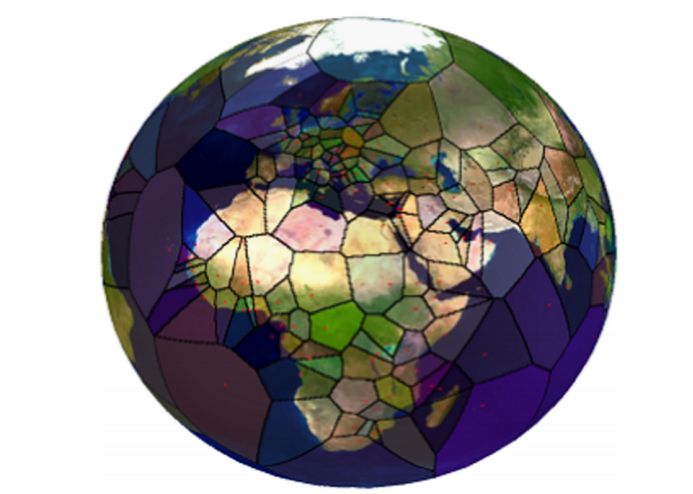
% R6 W4 V; m: ~( U 图2:基于WGS84椭球体上228个国家和地区的首都生成的Voronoi图
; [4 ?3 }6 F5 R S. t! [4 R" ^ (图片来源:PRESCHERN, 2012)
2 u) e5 b% X. o: Z! J" v: ^* a Voronoi图还被用于可视化其他连续性空间数据,也包括3D数据。而这些数据的传统处理方法主要是空间自相关和核密度方法等。在一个例子中显示,这些Voronois图有助于表明犯罪集中在哪里,以及展示了在哪些城市环境中的特定社区巡逻,警务工作可以获得最大的回报[7]。在其他情况下,Voronoi有助于区分人类活动的空间。例如,使用火车站作为点,这些车站内的活动密度产生一个空间,该空间具有给定的权重,然后用于定义相对于其他周边区域存在通勤交通的区域[8]。 8 }$ g, Q4 X' {% j8 h. q
对于典型的应用,Voronoi图可以由现在的许多GIS软件包创建。流行的软件包中,包括ArcGIS、GRASS和QGIS,都有用户社区或主要开发人员创建的插件。它广泛的应用领域表明,这类长期存在的方法将继续得到发展以改进它们的实现与计算,特别是对于复杂的空间和几何图形。 2 }9 s1 `& m ?+ [6 n! j
参考文献:
1 B( ^) }' H' E( { [1] For more on methods for voronoi calculations, see: Worboys, M. & Duckham, M. (2004) GIS: a computing perspective. 2nd ed. Boca Raton, Fla, CRC Press, pg. 190.
/ H# ]* ~ S, Q, j [2] For more on raster and vector tessellation, see: Chen, J. (1999) A raster-based method for computing Voronoi diagrams of spatial objects using dynamic distance transformation. International Journal of Geographical Information Science. [Online] 13 (3), 209–225. Available from: doi:10.1080/136588199241328. 8 V$ h2 _7 i& w( g" i8 L6 r
[3] For more on parallel algorithm approaches, see: Wang, J., Cui, C., Rui, Y., Cheng, L., et al. (2014) A parallel algorithm for constructing Voronoi diagrams based on point-set adaptive grouping: Parallel algorithm for voronoi diagrams. Concurrency and Computation: Practice and Experience. [Online] 26 (2), 434–446. Available from: doi:10.1002/cpe.3005.
( V: n( d! ^+ @( Y" @ [4] For more on tessellations using voroni methods on Earth’s surface, see:Hu, H., Liu, X. & Hu, P. (2014) Voronoi diagram generation on the ellipsoidal earth. Computers & Geosciences. [Online] 73, 81–87. Available from: doi:10.1016/j.cageo.2014.08.011. ! |5 j% m+ N6 H' g! q( R X
[5] For more on the crystal-growth tessellation, see: Wang, J., Kwan, M.-P. & Ma, L. (2014) Delimiting service area using adaptive crystal-growth Voronoi diagrams based on weighted planes: A case study in Haizhu District of Guangzhou in China. Applied Geography. [Online] 50, 108–119. Available from: doi:10.1016/j.apgeog.2014.03.001. 6 P3 x& p# X: ^
[6] For more on 3D GIS of voronoi visualization of cameras, see: Yaagoubi, R., Yarmani, M., Kamel, A. & Khemiri, W. (2015) HybVOR: A Voronoi-Based 3D GIS Approach for Camera Surveillance Network Placement. ISPRS International Journal of Geo-Information. [Online] 4 (2), 754–782. Available from: doi:10.3390/ijgi4020754. ) U2 T+ e5 S l' @2 Z7 j! C+ K1 f
[7] For more on the use of voronoi diagrams in crime observation and prevention, see: Melo, S.N. de, Frank, R. & Brantingham, P. (2017) Voronoi Diagrams and Spatial Analysis of Crime. The Professional Geographer. [Online] 69 (4), 579–590. Available from: doi:10.1080/00330124.2017.1288578.
9 q+ ~! H. X/ G0 u8 ^1 x: g [8] For more on voronoi calculations for rail activity, see: Mota, D.R., Takano, M. & Taco, P.W.G. (2014) A Method Using GIS Integrated Voronoi Diagrams for Commuter Rail Station Identification: A Case Study from Brasilia (Brazil). Procedia – Social and Behavioral Sciences. [Online] 162, 477–486. Available from: doi:10.1016/j.sbspro.2014.12.229.
H7 y+ h( L$ X$ I0 V+ s4 A 点击文末“阅读原文”即可查看原文章 7 y ^9 F/ G/ d5 I9 w, Y
 欢迎大家关注《慧天地》同名新浪微博 欢迎大家关注《慧天地》同名新浪微博
' Q; E# h' G. c5 a! Y4 Y$ L
微博ID:慧天地_geomaticser
9 O5 k% ]$ R/ g2 N  fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)
& P9 g. M5 U& Y& ]7 L7 }! }9 o m2 J
 fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)
' j5 z! Z& G. b

{9 c: B ?" a9 ]
荐读
" N0 c. ] _! ` 点击下文标题即可阅读
2 A- A1 z4 Y8 Y5 v' c4 @9 f 国际视野|看人工智能与众包地理信息如何解决遥感经典分类问题 0 _& N( m" {/ c: m. h
国际视野|助力联合国可持续发展目标:地理信息技术大有可为
9 \( ?1 M) Z8 }/ g# | m o0 V4 o3 C 分析与研究GIS数据的不确定性 / I" ?/ Y4 x) e5 ?
 fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)
6 g: Y; h$ G: v6 [- K
编辑 /黄松 审核 / 杜一鸣 张胜威
% }$ w5 `/ ]* j5 x+ y 指导:万剑华教授
3 i0 I, n7 S+ S% `- V# _7 Z; ]. R) P/ k
( k4 x1 B; p% o3 O$ w8 M
- W ~# K3 C! f5 U5 r9 s: ^5 N
% |: ~# W. Z/ K4 j! a | 

