|
( b/ S4 u1 Q9 d' W
人们描述空间中的一个点或者一个位置,通常会采用坐标这个概念。但是坐标或者坐标系怎么来的呢?需要怎么描述?它的参考是谁呢?又该怎么计算?  坐标(系)的几何来源6 W, \. V& a% z" ] 坐标(系)的几何来源6 W, \. V& a% z" ]
传说有这么个故事:有一天,笛卡尔(1596—1650年,法国哲学家、数学家、物理学家)生病卧床,但他头脑一直没有休息,在反复思考一个问题:几何图形是直观的,而代数方程则比较抽象,能不能用几何图形来表示方程呢?这里,关键是如何把组成几何的图形的点和满足方程的每一组“数”挂上钩。他就拼命琢磨。通过什么样的办法、才能把“点”和“数”联系起来。突然,他看见屋顶角上的一只蜘蛛,拉着丝垂了下来,一会儿,蜘蛛又顺着丝爬上去,在上边左右拉丝。 来源:百家号/创鹏科学堂  ; u- D: s2 D- O; u8 h* L7 s, j ; u- D: s2 D- O; u8 h* L7 s, j
蜘蛛的“表演”,使笛卡尔思路豁然开朗。他想,可以把蜘蛛看做一个点,它在屋子里可以上、下、左、右运动,能不能把蜘蛛的每个位置用一组数确定下来呢?他又想,屋子里相邻的两面墙与地面交出了三条线,如果把地面上的墙角作为起点,把交出来的三条线作为三根数轴,那么空间中任意一点的位置,不是都可以用这三根数轴上找到的有顺序的三个数来表示吗?反过来,任意给一组三个有顺序的数,也可以用空间中的一个点 P来表示它们。同样,用一组数(a, b)可以表示平面上的一个点,平面上一个点也可以用一组二个有顺序的数来表示。于是在蜘蛛的启示下,笛卡尔创建了直角坐标系。 来源:百家号/创鹏科学堂  把图形看成点的运动轨迹,这个想法很重要!它从指导思想上,改变了传统的几何方法!随着笛卡尔解析几何的推广,坐标系也逐渐被改进与完善。范斯库藤(Frans van Schooten,1615-1660),为笛卡尔坐标方法的推广起到了关键作用,还给出了坐标变换——从一条基线(x轴)到另一条基线变换的代数式;沃利斯(John Wallis, 1616-1703)在坐标系上的贡献在于他引入了负坐标,将坐标几何的研究由第一象限推广到了四个象限;再后来牛顿又用了沃利斯的坐标体系,使得解析几何有了快速的普及。雅各布·伯努利(JakobI. Bernoulli, 1654-1705)于1691年在《教师学报》上发表了有关极坐标的成果,发明了极坐标。17世纪中后期,由拉伊尔(Philippede La Hire, 1640-1718)、约翰·伯努利(JohannBernoulli, 1667-1748)、帕朗(Antoine Parent,1666-1716)、欧拉(Leonhard Paul Euler, 1707-1783)等人的工作,将平面坐标系发展为空间三维坐标系。 把图形看成点的运动轨迹,这个想法很重要!它从指导思想上,改变了传统的几何方法!随着笛卡尔解析几何的推广,坐标系也逐渐被改进与完善。范斯库藤(Frans van Schooten,1615-1660),为笛卡尔坐标方法的推广起到了关键作用,还给出了坐标变换——从一条基线(x轴)到另一条基线变换的代数式;沃利斯(John Wallis, 1616-1703)在坐标系上的贡献在于他引入了负坐标,将坐标几何的研究由第一象限推广到了四个象限;再后来牛顿又用了沃利斯的坐标体系,使得解析几何有了快速的普及。雅各布·伯努利(JakobI. Bernoulli, 1654-1705)于1691年在《教师学报》上发表了有关极坐标的成果,发明了极坐标。17世纪中后期,由拉伊尔(Philippede La Hire, 1640-1718)、约翰·伯努利(JohannBernoulli, 1667-1748)、帕朗(Antoine Parent,1666-1716)、欧拉(Leonhard Paul Euler, 1707-1783)等人的工作,将平面坐标系发展为空间三维坐标系。 地球椭球与坐标系无论是科学、工程还是数学领域,直角坐标都扮演着重要的角色。它是描述三维空间中点的位置的有效方法,并为我们提供了一种全面而清晰的方式来分析和应用空间中的各种现象。在测绘中,坐标系又是怎样定义的呢?为了表示地球上每一个点的位置,是不是要建立一个统一的世界坐标系呢?又是怎样确定坐标原点和坐标轴呢?让我们带着上述的问题来寻找答案。首先,既然是坐标系,那一定是建立在一个对象上面。那这个对象是什么呢?没错,就是我们生活的地球。地球的表面几何模型主要有3类:01地球天然表面大家知道,地球的天然表面是一个崎岖不平的曲面,有高山、平原、盆地、丘陵和海洋等。大陆上的世界最高峰珠穆朗玛峰高出平均海水面8848.86m,大洋最深处在北太平洋西部海床的马里亚纳海沟低于平均海水面11022m,两点高差大约20000m。所以地球天然表面难以用简单的数学表达式描述,不适宜数字建模,因而不能作为测量和地图制图的基准面。 地球椭球与坐标系无论是科学、工程还是数学领域,直角坐标都扮演着重要的角色。它是描述三维空间中点的位置的有效方法,并为我们提供了一种全面而清晰的方式来分析和应用空间中的各种现象。在测绘中,坐标系又是怎样定义的呢?为了表示地球上每一个点的位置,是不是要建立一个统一的世界坐标系呢?又是怎样确定坐标原点和坐标轴呢?让我们带着上述的问题来寻找答案。首先,既然是坐标系,那一定是建立在一个对象上面。那这个对象是什么呢?没错,就是我们生活的地球。地球的表面几何模型主要有3类:01地球天然表面大家知道,地球的天然表面是一个崎岖不平的曲面,有高山、平原、盆地、丘陵和海洋等。大陆上的世界最高峰珠穆朗玛峰高出平均海水面8848.86m,大洋最深处在北太平洋西部海床的马里亚纳海沟低于平均海水面11022m,两点高差大约20000m。所以地球天然表面难以用简单的数学表达式描述,不适宜数字建模,因而不能作为测量和地图制图的基准面。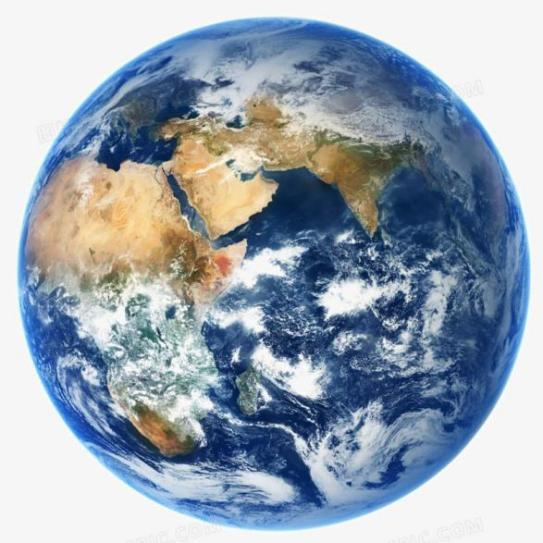
% I, U: q( S9 H+ }8 b 来源:千图网 02大地水准面地球被称为水球,因为地球表面72%被海水覆盖。假设当海水处于完全静止的平衡状态时,大地水准面是从海平面延伸到所有大陆下部,而与地球重力方向处处于正交的一个连续、闭合的水准面。上述概念是什么意思呢?通俗来说是指,地球自然表面凹凸起伏,设想海洋只受到重力的影响,静止不动,我们把海水面延伸到大陆上去,形成包围整个地球的连续表面,这个静止的平均海水面会穿过大陆和岛屿形成一个闭合的曲面,现在我们假设存在这样一个几何表面,它与重力方向相垂直,又与这个静止的平均海水面相重合,这个几何表面就叫做大地水准面。由于地质条件等因素,大地水准面局部存在不规则起伏,在测量和GIS应用上较困难。03地球椭球面5 i% j# t% [, U/ l) ]' t
因为大地测量和地图制图等地理信息工作需要在一个规则严密的几何参考面上才能进行各种测量计算和制图表达,所以前人用一个非常接近于大地水准面,并可用数学式表示的几何形体来代替地球的形状,作为测量计算工作的基准面。地球是一个两极稍扁赤道略鼓的不规则椭圆球体,于是基准面采用的是一个椭圆绕其短轴旋转而成的形体,即地球椭球,又称旋转椭球。
; Y5 E9 _7 K+ t$ Q3 l 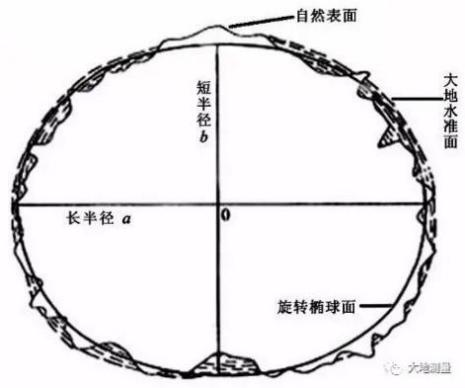
6 d' K3 ~! S; s3 S 来源:微信公众号:大地测量 # f. a& d$ m+ P/ Q! U
地球椭球的长轴、短轴测定后,还必须确定大地水准面与椭球体面的相对关系。即确定与局部地区大地水准面符合最好的一个地球椭球体---参考椭球体,这项工作就是参考椭球体定位。在测量学中,坐标系分为两大类,参心坐标系和地心坐标系。 , K# C5 ?" `0 i! Q
参心坐标系是以参考椭球体的几何中心为原点的大地坐标系。“参心”意指参考椭球的中心。通常分为参心空间直角坐标系(以X,Y,Z为其坐标元素)和参心大地坐标系(以B,L,H为其坐标元素)。参心坐标系是在参考椭球体内建立的O-XYZ坐标系。原点O为参考椭球体的几何中心,X轴与赤道面和首子午面的交线重合,向东为正。Z轴与旋转椭球的短轴重合,向北为正。Y轴与XZ平面垂直构成右手系。参心大地坐标系的应用十分广泛,它是经典大地测量的一种通用坐标系。根据地图投影理论,参心大地坐标系可以通过高斯投影计算转化为平面直角坐标系,
- w* v- B4 p8 }5 o6 I 
3 I3 w4 e7 F5 A( U# A; e( J
来源:CSDN 地心坐标系是以地球质心为原点建立的空间直角坐标系。通常分为地心空间直角坐标系(以X,Y,Z为其坐标元素)和地心大地坐标系(以B,L,H为其坐标元素)。地心坐标系是在大地体内建立的O-XYZ坐标系。原点O设在大地体的质量中心,用相互垂直的X,Y,Z三个轴来表示,X轴与首子午面与赤道面的交线重合,向东为正。Z轴与地球旋转轴重合,向北为正。Y轴与XZ平面垂直构成右手系。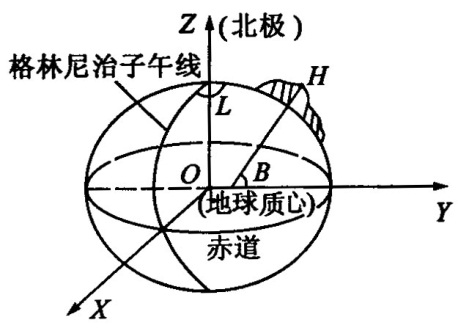
, ?/ n3 K- m+ ~* Q$ g) [ 来源:CSDN  我国常用的坐标系统根据上述介绍的地球椭球面和参考椭球体,各个国家会根据自身的地貌特征去设置不同的参考椭球体,基于不同椭球、不同定位和定向参数,可以构建不同的坐标系统。我国使用过的或常用的国家大地坐标系统有1954年北京坐标系、1980西安坐标系及2000国家大地坐标系。 我国常用的坐标系统根据上述介绍的地球椭球面和参考椭球体,各个国家会根据自身的地貌特征去设置不同的参考椭球体,基于不同椭球、不同定位和定向参数,可以构建不同的坐标系统。我国使用过的或常用的国家大地坐标系统有1954年北京坐标系、1980西安坐标系及2000国家大地坐标系。 1954年北京坐标系新中国成立以后,我国大地测量进入了全面发展时期,在全国范围内开展了全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系。由于当时的“一边倒”政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。 1954年北京坐标系新中国成立以后,我国大地测量进入了全面发展时期,在全国范围内开展了全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系。由于当时的“一边倒”政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。1954年北京坐标系,长半轴a=6378245m,扁率α=1/298.3,属于参心坐标系。原点不在北京,而是在前苏联的普尔科沃。  1980西安坐标系
5 c0 y% [7 C3 {" X. J1 n# I 1980西安坐标系
5 c0 y% [7 C3 {" X. J1 n# I 1978年4月在西安召开全国天文大地网平差会议,确定重新定位,建立我国新的坐标系。椭球参数采用的是IUGG1975年推荐的椭球参数。椭球定位和定向的条件是: 椭球短轴平行于地球地轴(由地球质心指向 1968.0JYD地极原点方向) ;首子午面平行于格林尼治平均天文子午面;椭球面同似大地水准面在我国境内最密合,按我国范围内高程异常值平方和最小为原则求解参数。1980西安坐标系,长半轴a=6378140m,扁率α=1/298.257,属于参心坐标系。原点在陕西省泾阳县永乐镇石际寺村,具体位置:北纬34°32′27″,东经108°55′25″,海拔高度417.20m。
7 U' ]( j8 {2 V% l, A& t 
" @* A' t$ m4 f5 d. E4 C
来源:微信公众号:测绘之家  2000国家大地坐标系2008年7月1日,经国务院批准,我国正式启用2000国家大地坐标系(CGCS2000)。X轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点;Z轴由原点指向历元2000.0的地球参考极的方向;Y轴与Z轴、X轴构成右手正交坐标系。该历元的指向由国际时间局给定的历元1984.0。 2000国家大地坐标系2008年7月1日,经国务院批准,我国正式启用2000国家大地坐标系(CGCS2000)。X轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点;Z轴由原点指向历元2000.0的地球参考极的方向;Y轴与Z轴、X轴构成右手正交坐标系。该历元的指向由国际时间局给定的历元1984.0。2000国家大地坐标系,长半轴a=6378137m,扁率α=1/298.257222101,属于地心坐标系,原点为包括海洋和大气的整个地球的质量中心。2018年7月1日起自然资源系统全面开始使用2000国家大地坐标系,其他行业系统也逐渐全面应用。  坐标系形式及坐标转换
! ?9 H+ [4 \+ R/ |4 j 坐标系形式及坐标转换
! ?9 H+ [4 \+ R/ |4 j 人们为了描述空间位置,采用了多种方法,也产生了不同的坐标系(形式),如直角坐标系、极坐标系、球坐标系等。
1 }+ r" Z0 }- O 在测量中,地心坐标系和参心坐标系都有下列几种表达形式:空间直角坐标系、空间大地坐标系及平面直角坐标系。 1空间直角坐标系 T( a! Y) s* I* b) [5 D
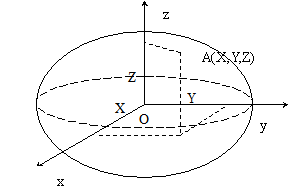
[9 p7 Y% _& h" X( m* |
来源:微信公众号:GISerliang与0和1 6 S+ ?7 b. Q2 D! u4 J) r
空间直角坐标系的坐标系原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上,且按右手系与X轴呈90夹角。某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。 2空间大地坐标系 - n, I! u0 v- O. K" M+ f - n, I! u0 v- O. K" M+ f
来源:CSDN , I& V: C- {, [/ @
空间大地坐标系是采用大地经度(L)、大地纬度(B)和大地高(H)来描述空间位置的。纬度是空间点与参考椭球面的法线与赤道面的夹角,经度是空间点与参考椭球自转轴所在的面与参考椭球的起始子午面的夹角,大地高是空间点沿参考椭球的法线到参考椭球面的距离。 3平面直角坐标系 9 v+ c" m! a- |# |" C
9 v+ c" m! a- |# |" C 来源:微信公众号:测绘玩家 , v u6 t% H- v, ^1 p4 f" n2 ]
9 S" f# H+ y' h& G
来源:百度百科
" Y3 i8 m; ~' _8 T5 e* k 在参考椭球面的基础上建立的空间坐标(空间直角坐标或空间大地坐标),在地球科学研究、航空航天、卫星导航定位等方面有着广泛应用。 1 F7 h* @& ?3 D; S
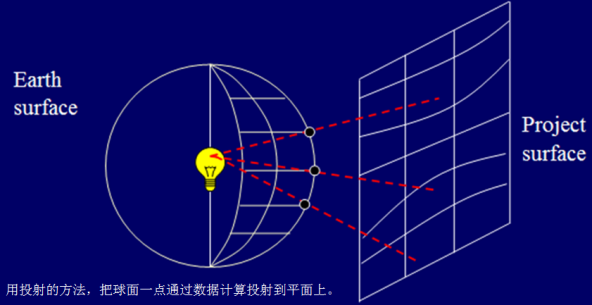
但在一般的道路工程、工程测量等应用中并不直接使用地理坐标,而是将地球表面或者参考椭球面上的元素(坐标、距离、方位等)通过一定数学法则投影到平面上,建立地面上的点与平面上的点一一对应的关系,这样才能反映出点之间的位置、方向、面积、大小、距离、形状及数量关系,这就是地图投影的过程。这种将空间坐标(空间直角坐标或空间大地坐标)通过某种数学变换映射到平面的变换,称为投影变换,投影变换后即形成了平面直角坐标系。
, }1 ?7 d* x$ U/ o2 V% [ 投影变换的方法有很多,如UTM投影、Lambuda投影等。我国采用的是高斯-克吕格投影,属于等角横切椭圆柱投影,投影后的建立平面直角坐标系统简称为高斯直角坐标系。 4坐标转换! O0 r2 j9 b; @2 A9 M. [7 Z. N
坐标系形式变换。同一个坐标系统下,点位坐标形式有空间大地坐标(B,L,H)、空间直角坐标(X,Y,Z)、平面直角坐标(x,y)等形式,坐标变换指的就是同一个点、在相同椭球体下各种坐标形式之间的变换。
' a- V8 b5 O. B+ A 由前述可知,各种坐标量均为基于规则严密的几何参考面的数学表达。因此,很显然,在参考椭球及投影方式确定的情形下,坐标变换只是几何关系的一种数学变换,可用公式表达,理论上应该是无缝的、且精确可逆的。实际亦如此,比如已知某点在2000国家大地坐标系下的空间直角坐标,即可直接坐标变换计算得到该点的空间大地坐标、或中央经度线下的平面直角坐标,而坐标变换得到的空间大地坐标再进行坐标变换到空间直角坐标,理论上与已知的空间直角坐标会完全一致。
& [. } t9 J3 E; s7 } 不同坐标系统间转换。一种坐标系统变换到另一种坐标系统的过程,其实质是同一个点在不同椭球体下表达的转换,是通过建立两个坐标系统之间一一对应关系来实现,通常采用相似变换的方法。要实现高精度的转换,通常需要转换区域一定数量的重合点(同时具有源坐标及目标坐标,且坐标形式一样),选用合适的数学模型,采用最小二乘的方式拟合计算出转换模型的各项参数,参与点位的转换残差等。 4 ]# @& `# h( n8 b9 A) Z% [8 j0 a
(1)基于平面直角坐标的转换模型 , h1 C- D+ t" z: Q4 L5 e4 m* l! y
平面直角坐标系下的二维转换,采用四参数转换模型。 ( \4 s6 f7 r/ | X6 Z
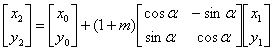
7 }, P) u( Y2 D5 d/ U
其中,x₀,y₀为平移参数,α为旋转参数,m为尺度参数。x₁,y₁为原坐标系下平面直角坐标,x₂,y₂为目标坐标系下的平面直角坐标,坐标单位为米。
$ s3 P2 _- `/ `2 z" C4 M1 I (2)基于空间直角坐标的转换模型 & u/ H* U2 X3 f. g; U# C: U1 Y/ Q
空间直角坐标系下的三维转换,通常采用布尔莎转换模型。 4 d8 V- [* | a
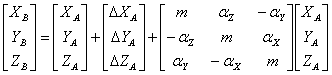
# p' c/ s% b' U5 z! `
其中:7个转换参数——3个平移参数,一个尺度参数,三个旋转参数。为原坐标系下空间直角坐标,为目标坐标系下的空间直角坐标,坐标单位为米。 7 M2 D# I& T2 ^. e3 o/ v
(3)基于空间大地坐标的转换
) o/ y' v* a u( c1 @6 N& i, Z 一般采用改正数法,采用广义大地坐标微分公式直接求出大地坐标改正数。坐标转换考虑了不同坐标系椭球参数的变化,有二维七参数法及三维七参数法,适用于不同大地坐标系间的转换。  高斯投影与独立坐标系 M* |' s! T% ? 高斯投影与独立坐标系 M* |' s! T% ?
地球椭球面是一个不可展的曲面,而地图是一个平面,把不可展的地球椭球曲面上的元素通过地图投影绘制成平面的图形,避免不了产生各种变形。因此,我国在地图制图和地理信息工作中,为了减小长度变形,采用了高斯投影分带的方法,主要采用3°带和6°带进行高斯投影分带,1:2.5万至1:50万的地形图采用6°带;1:1万及更大比例尺图采用3°带。 来源:微信公众号:测绘玩家 fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)  fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E) ) L7 J% B# V/ R5 R
) L7 J% B# V/ R5 R 但在局部地区进行工程测量和大比例尺制图时,如果采用2000国家大地坐标系坐标椭球,在国家标准的3°带高斯投影下,长度变形值会超出规定的误差区间(相关国家及行业标准规范通常要求投影长度变形不大于2.5cm/km),这需要通过建立相对独立的平面坐标系统(简称独立坐标系)。独立坐标系是2000国家大地坐标系的必要补充。
( R, Z( a. P- _/ I7 l1 } 独立坐标系分为城市坐标系和工程坐标系。由政府部门组织建立的在一定行政区划范围内通用的独立坐标系属于城市坐标系;因重大工程项目建设需要,由工程建设单位组织建立的独立坐标系属于工程坐标系。城市坐标系的设立,一般兼顾城市区域的发展,总体考虑投影变形不超过2.5cm/km的区域占全市的比例及对变形超限区域带来的影响;工程坐标系的设立为满足工程区域建设应用,考虑应用时各观测点位长度变形能满足要求即可。
?& G- W6 X+ X* H2 Z 对于坐标系,大家都明白了吗? 参考文献$ b/ m2 E, t, J5 p/ q
[1]自然资源部关于印发《建立相对独立的平面坐标系统管理办法》的通知(自然资规〔2023〕5号) 7 c8 F1 b$ j2 `2 b
[2]宋巧巧.坐标系是如何“诞生”的[J].语数外学习(高中版下旬),2022,806(09):61-63.
6 P7 X- M9 [4 | [3]王忠礼,刘德利.测绘领域中常用坐标系统及其转换计算[J].吉林建筑大学学报,2021,38(05):34-38.
- n& N6 h5 @3 {- r) y( l7 z- h4 R0 Q2 t [4]谢春雨.地质图常用地图投影变形特征分析[J].海洋石油,2015,35(02):30-34.
7 l( W, ^" g; j! _* i6 v [5]高飞,李鹏.1980西安坐标系向CGCS2000国家大地坐标系转换方法研究及应用[J].云南冶金,2021,50(04):1-4. ; a/ Y( |% b* ?8 w3 [
( Q9 h4 [7 j) z0 {: l: x+ w -----END-----
6 r7 ]+ B- x: ?7 } 来源:广东省国土资源测绘院 ) P; Q, I, ~, h; S( U
转自:测绘之家  fill=%23FFFFFF%3E%3Crect x=249 y=126 width=1 height=1%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E) / e6 w: X, ~, M) h& A. H1 I
/ e6 w: X, ~, M) h& A. H1 I ●地籍调查工作!自然资源部印发通知,明确这些要求
+ ^% m( _. m- b; t2 W$ m( v+ W: L ●国家林草局答复:“三调”中的其他草地应按草原进行管理 + g1 {+ s5 C* {. C! i0 [6 B
●耕地保护红线决不能触碰
a; {$ W9 t8 m8 G ●既保障资源要素,又严守红线底线,怎么理解这些政策?
+ b4 M2 t8 u. {/ E7 H# j' v, A
' m' E( r+ _8 W% x8 Y
6 e' E4 {" H( K3 [# ~* X! S% E! o$ |; q$ r8 A2 o
, y' H5 H$ {9 W% d
9 J4 K5 d! B. y: c F7 Z5 c( I4 h | 

