山东大学在海洋牧场工程和生态学领域取得新进展 - 海洋生物生态学研究

8 E/ o$ k& N N m/ j: ^6 `2 t

/ r3 N, Q' [9 h

      近日，山东大学梁振林教授团队在海洋牧场工程与生态学领域取得系列进展，为现代化海洋牧场的建设和发展提供参考，相关成果发表在Science of the Total Environment、Ocean Engineering、Marine Pollution Bulletin等期刊。

      （1）“鱼类全生活史”型海洋牧场构建

      海洋牧场是一种新型的海洋渔业生产方式，休闲垂钓型海洋牧场是其重要的组成部分。在系统梳理休闲垂钓型海洋牧场研究和产业发展现状的基础上，针对我国休闲垂钓型海洋牧场成鱼补充量不足的问题，提出构建“鱼类全生活史”型海洋牧场的理念和相关技术，即以“产卵—仔稚鱼—幼鱼—成鱼”为保护链，在同一海洋牧场区域内完成鱼类全部生活史，恢复鱼类资源、增加生物多样性的同时，又能为休闲垂钓型海洋牧场建设的发展起到示范作用。2018年在威海市双岛湾附近海域构建了我国首个“鱼类全生活史”型海洋牧场试验点，为5个“国家级海洋牧场示范区”和2个“山东省级海洋牧场示范区”建设提供技术支持，并为合作企业争取到国家、省级财政补贴资金超亿元。

      （2）生态型人工鱼礁结构设计

/ O ?, W6 I; k8 q. |. N) @% b

      人工鱼礁是海洋牧场建设中重要的基础生态工程，是改善海洋生态环境，保护海洋生物资源的重要措施。为了完善修复和养护上述研究链条中的成鱼栖息地，团队以立方礁为研究对象，基于计算流体力学方法，开展了诸多生态型人工鱼礁的结构设计与优化工作。上述研究成果以“Effect of hole diameter of rotary-shaped artificial reef on flow field”和“Research on the influence of cut-opening factors on flow field effect of artificial reef”为题，发表在Ocean Engineering。硕士研究生聂兆一为第一作者，梁振林教授和姜昭阳教授为并列通讯作者。

      （3）海洋牧场低氧灾害

2 }1 @4 Q/ C8 F2 \

      在上述生态型鱼礁结构优化的基础上，针对中国黄海北部沿岸海洋牧场夏季海水极度低氧现象而导致的人工鱼礁区刺参大规模死亡灾害现象，开展了生态型人工鱼礁建设，对低氧现象起到了一定的缓解作用。同时，探究了该区域微生物群落结构及其影响因素，为理解微生物群落对海洋牧场季节性低氧的响应机制提供基础数据，对海洋牧场的管理和保护具有重要意义。上述研究成果以“Response mechanism of microbial community to seasonal hypoxia in marine ranching”为题，发表在Science of the Total Environment。硕士研究生王璐为第一作者，姜昭阳教授为通讯作者。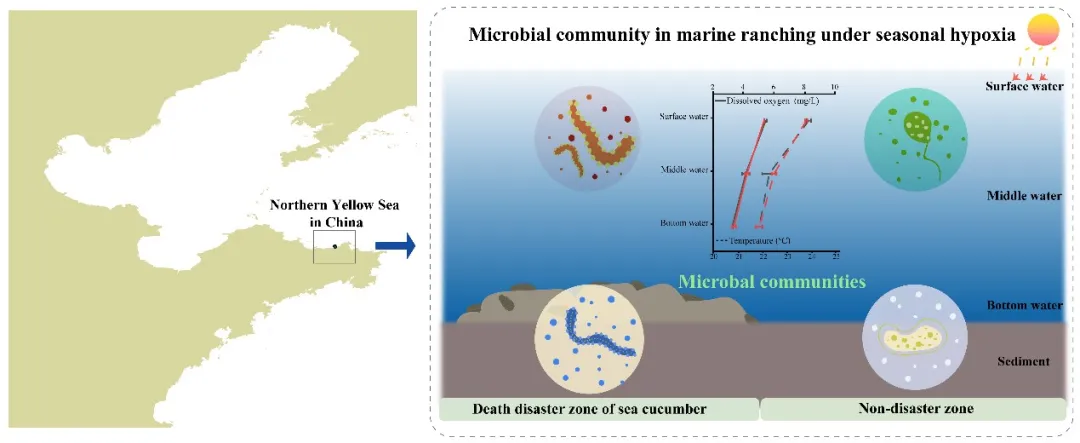

9 `2 M* y, o# T" j* o" }

      （4）海洋牧场微生态

      在宏观生态环境监测的基础上，探究礁区微生物群落结构特征将有助于深入了解人工鱼礁的生态效应。通过比较人工鱼礁不同材质、岩礁附着的优势大型海藻表面的微生物群落结构，结合环境因子，解析微生物群落结构和多样性动态变化特征、微生物群落之间的相互作用，为人工鱼礁建设生态效果评估提供了理论依据。上述研究成果以“Comparison studies of epiphytic microbial communities on four macroalgae and their rocky substrates”、“Comparative Analysis of the Ecological Succession of Microbial Communities on Two Artificial Reef Materials”为题，分别发表在Marine Pollution Bulletin和Microorganisms。实验师郭战胜为第一作者，梁振林教授和姜昭阳教授为并列通讯作者。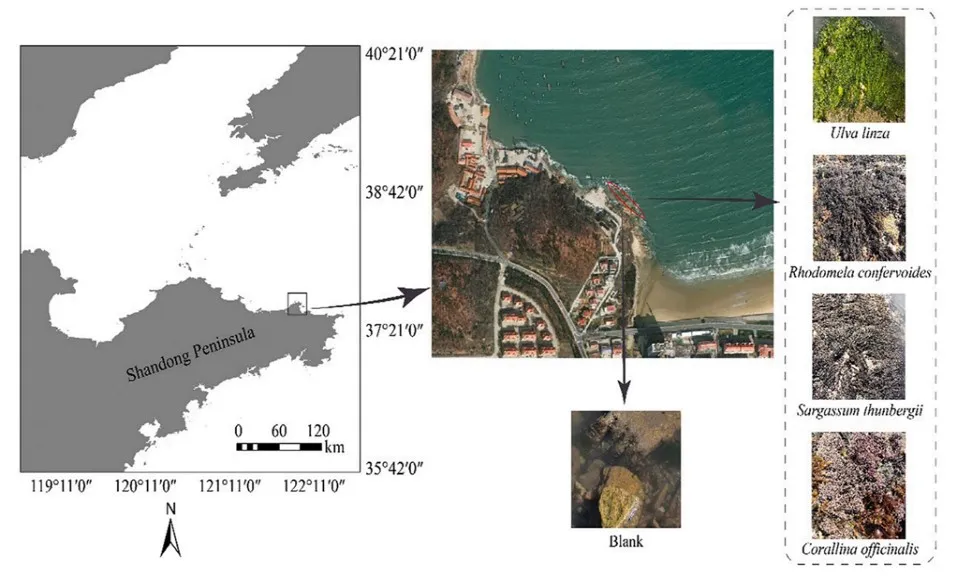

上述研究工作得到了国家重点研发计划 (2016YFE0205700) 、国家自然科学基金 (42176150 和41771544)等的资助。

本文来源：山东大学（威海）

5 v+ p: k, ?- m

1 u( x5 U7 w" X ? K, h